Чотирикутники

Mere som dette

Ламана Многокутник і його елементи Сума опуклих кутів многокутника

af Killa queen BAIT ZA DASTO

Площі фігур

af Анастасия Поливода

Площадь

af Анна Яганина

Логотип бренду одягу

af Дар`я Олександрівна Рижова

Чотирикутник — фігура, яка складається з чотирьох точок (жодні три з них не лежать на одній прямій) і чотирьох відрізків, які з'єднують послідовно ці точки і не перетинаються.

Прямокутник

Прямокутник — це чотирикутник, усі кути якого прямі. Протилежні сторони прямокутника рівні. Є окремим випадком паралелограма. Також його можна визначити як чотирикутник із чотирма однаковими кутами, оскільки це означатиме, що всі його кути будуть прямими (360°/4 = 90°). Також це паралелограм, який має прямий кут (а отже, всі кути прямі). Прямокутник, в якого всі чотири сторони мають однакову довжину, називають квадратом.

Довшу сторону прямокутника називають довжиною прямокутника, а коротшу — шириною прямокутника

If you already did 4 pomodoros, take a longer break, between 15-30 minutes. In this break you can go for a walk, eat something, do a short circuit of exercises, etc.
Plan your breaks ahead!

Схрещенні прямокутники

Схрещений прямокутник (такий, що перетинає сам себе) складається із двох протилежних сторін звичайного прямокутника і двох діагоналей. Схрещений прямокутник, так само, є різновидом схрещеного чотирикутника. Він має той самий порядок вершин. Він представлений двома ідентичними трикутниками із спільною вершиною, але геометричний перетин не розглядається як вершина.

Схрещений чотирикутник іноді асоціюють із краваткою-метеликом або формою метелика. Тривимірну прямокутну каркасну конструкцію із дроту можна скрутити таким чином, що вона прийме форму метелика. Схрещений прямокутник іноді називають "кутовою вісімкою".

Схрещений прямокутник не є рівнокутним. Сума його внутрішніх кутів (двох гострих і двох розгорнутих кутів), як і в будь-якого схрещеного прямокутника, дорівнює 720°.[9]

Прямокутник і схрещений прямокутник є чотирикутниками, що мають наступні спільні властивості:

Протилежні сторони мають однакову довжину.
Дві діагоналі мають однакову довжину.

Фітнес для мізків. Склади прямокутник

Основні властивості

Властивості прямокутника

Діагоналі прямокутника рівні.
Діагоналі прямокутника перетинаються і точкою перетину діляться навпіл.
Діагоналі прямокутника ділять його на два рівні трикутники.
Висоти прямокутника є одночасно і його сторонами.
Навколо будь-якого прямокутника можна описати коло, причому діагональ прямокутника дорівнює діаметру даного кола.
Квадрат діагоналі прямокутника дорівнює сумі квадратів двох його не протилежних сторін.
Прямокутник є плоскою геометричною фігурою, його аналогом у тривимірному просторі є прямокутний паралелепіпед.

Описані та вписані чотирикутники

Якщо всі сторони чотирикутника дотикаються до кола, то він називається чотирикутником, описаним навколо кола, а коло — вписаним у чотирикутник.

Чотирикутник, усі вершини якого лежать на колі, називається вписаним у коло, а коло називається описаним навколо чотирикутника.

Розберемось?!

Вписаний чотирикутник

В Евклідовій геометрії вписаний чотирикутник — це чотирикутник, вершини якого лежать на одному колі. Центр кола та його радіус називають центром окружності та окружністю.

Усі трикутники можна вписати в коло, але не кожен чотирикутник можна вписати в коло.

Будь-який квадрат, прямокутник, і рівнобедрену трапецію можна вписати в коло.

Опуклий чотирикутник ABCD можна вписати тоді і лише тоді, коли його протилежні кути є суміжними, тобто

Описаний чотирикутник

В чотирикутник можна вписати коло тоді й тільки тоді, коли суми його протилежних сторін рівні.

Трапеція

Трапецією називається чотирикутник, дві протилежні сторони якого паралельні, а дві другі не паралельні.

Існують рівнобічні, прямокутні та власне трапеції.

*Паралельні сторони називаються основами трапеції, а дві інші – бічними сторонами.

! Діагоналі в точці перетину не діляться навпіл і вони не перпендикулярні.

*Висота – це перпендикулярна відстань між основами.

Основні властивості трапеції

1. В трапецію можна вписати коло, якщо сума довжин основи рівна сумі довжин бокових сторін:

AB + CD = BC + AD

2. Середня лінія трапеції розділяє навпіл будь-який відрізок, який з'єднує основи,а також ділить навпіл діагоналі:

AK = KB, AM = MC, BN = ND, CL = LD

3. Середня лінія трапеції паралельна основам і рівна їх півсумі:

m = (a + b):2

4. Точка перетину діагоналей трапеції і середини основ лежать на одній прямій.

5. В трапеції бокову сторону видно із центра вписаного кола під кутом 90°.

6. Кожна діагональ в точці перетину ділиться на дві частини з таким співвідношенням довжини, як співвідношення між основами:

BC : AD = OC : AO = OB : DO

7. Діагоналі трапеції d₁ і d₂ пов'язані зі сторонами співвідношенням:

d₁² + d₂² = 2ab + c² + d²

Усе про трапецію

З історії виникнення поняття «трапеція»

Слово «трапеція» походить від грецького слова τραπέζιον — «столик». Цей термін і слово «трапеза» (грецькою τράπεζα) мають спільне походження, тобто слово «трапеза» дослівно означає «стіл, їжа». Термін трапеція спочатку застосовувався в розумінні будь-якого чотирикутника і лише у XVIII столітті набув сучасного змісту. Деякі властивості елементів трапеції були вже відомі стародавнім єгиптянам і вавилонським землемірам. Єгиптяни вміли обчислювати площу трапеції. Вавилонські математики про трапецію говорили «лоб бика».

Багатозначність терміну «трапеція»

Термін «трапеція» - є багатозначним.

Трапеція — це чотирикутник, дві протилежні сторони якого паралельні.
Криволінійна трапеція - фігура на площині, обмежена графіком невід'ємної неперервної функції у=f(х), визначеною на відрізку [a; b], віссю абсциса і прямими х=а та х=b, яка широко використовується у зачах фізичного та хімічного змісту.
Трапеція – це гімнастичний прилад, що складається з горизонтальної поперечки, підвішеної на двох тросах або мотузках.
Трапеція — гірська вершина на Уралі. Трапеція — японський мультфільм (аніме, психологічна драма).
Трапеція — номенклатурний аркуш топографічної карти (Її рамки – трапеції, утворені меридіанами й паралелями, проведеними відповідно через 6° довготи і 4° широти).
Трапеція Оріона, або Скупчення Трапеція Оріона є компактним розсіяним скупченням зір, що розташоване у самому серці Туманності Оріона. Воно було відкрито Галілео Галілеем 4 лютого 1617 року, коли він замалював відносне розташування трьох зір трапеції (A, C, D).

Трапецію можна побачити у багатьох плоских та просторових геометричних фігурах.

Де та як знайти середню лінію трапеції

Середня лінія - відрізок, що з'єднує середини бокових сторін трапеції.

Формули визначення довжини середньої лінії трапеції:

1. Формула визначення довжини середньої лінії через довжини основ:

m = (a + b):2

2. Формула визначення довжин середньої лінії через площу та висоту:

m = S:h

Квадрат

Квадрат — чотирикутник, у якого всі сторони рівні і всі кути прямі. Для побудови квадрата необхідно і достатньо задати дві точки на координатній площині, які відповідатимуть будь-яким двом кутам і врахувати їхню суміжність.

Квадрат є водночас ромбом та прямокутником і навпаки: кожна фігура, яка є водночас ромбом і прямокутником, є квадратом

After each pomodoro do a 5 minute break! In these 5 minutes, think of/do anything but the task.
You can add your ideas for the 'lightning' breaks: it can be a 5-minute stretching, reading a short article, etc.

Магазин головоломок

Дуже часто квадрат використовують у різноманітних головоломках.

Загадка зниклого квадрата — це оптична ілюзія, що часто використовується на уроках математикидля пояснення властивостей геометричних фігур. Вона зображає дві фігури, складені з однакових частин, але в різному порядку, на вигляд прямокутні трикутники із катетами відношенням 13 до 5. Але один із них містить прогалину — квадрат 1х1.

Згідно з Мартіном Гарднером, головоломку придумав нью-йоркський фокусник-аматор Поль Керрі у 1953. Відтоді загадка була відома під назвою «Парадокс Керрі», хоча рішення було відоме ще з XVI століття.

Розв'язок

«Гіпотенузи» 13×5 «трикутників» насправді є ламаними лініями, які утворюють паралелограм

Ключем до загадки є те, що жодний із 13×5 «трикутників» не має ту ж саму площу, що й площа їх складових.

Сумарна площа чотирьох фігур (жовтої, червоної, синьої та зеленої) становить 32 одиниці площі, але довжини сторін трикутників 13 та 5, що відповідно становить 32,5 квадратних одиниць. Відношення катетів синього трикутника 5:2, а червоного 8:3. За ознакою подібності прямокутних трикутників випливає що ці трикутники не подібні, а значить мають різні відповідні гострі кути. Отже, видимі складені «гіпотенузи» великих «трикутників», насправді є ламаними.

Кут нахилу гіпотенуз червоного та синього трикутників до гіпотенузи 13×5 трикутника дуже малий і його важко помітити неозброєним оком. Але якщо придивитись, то видно, що точка стику гіпотенуз червоного та синього трикутників, формує тупий кут, що трішки вигнутий вгору (назовні) нижнього «трикутника» і тупий кут вигнутий вниз (всередину) верхнього «трикутника». Якщо накласти «гіпотенузи» обох фігур, то утвориться паралелограм, площею рівною одному квадратику.

Довжини сторін фігур з даної задачі (2, 3, 5, 8, 13) є послідовними числами Фібоначчі.

Квадрат у задачах

Формули, пов'язані з квадратом

• Чорний колір — квадрат,

• Блакитний колір: описане коло;

• Коричневий колір: вписане коло

Якщо $a$ — довжина сторони квадрата, тоді

Площа квадрата: $S = a^2$
Довжина діагоналі: $d=a{\sqrt {2}}$
Радіус вписаного кола: $r = \frac{a}{2}$
Радіус описаного кола: $R = \frac{\sqrt 2}{2} a$
Периметр квадрата: $P = 4 a = 4 \sqrt 2 R = 8 r$

Квадрат та його властивості

Властивості квадрата

У квадрат завжди можна вписати коло;
Навколо квадрата завжди можна описати коло.
Як і в будь-якого опуклого чотирикутника, в квадрата:
Сума всіх внутрішніх кутів дорівнює 2π (360°).

Як і в будь-якому прямокутнику:

Протилежні сторони паралельні.
Діагоналі діляться точкою перетину навпіл.
Точка перетину діагоналей є центром симетрії квадрата.
Діагоналі рівні між собою.

Як і в будь-якому ромбі:

Діагоналі є бісектрисами кутів.
Діагоналі перетинаються під прямим кутом.
Діагоналі є осями симетрії.

Паралелограм

Паралелограм — чотирикутник, протилежні сторони якого попарно паралельні.

Існує декілька окремих видів паралелограма:

Прямокутник — паралелограм, всі кути якого прямі;
Ромб — паралелограм, всі чотири сторони якого рівні між собою;
Квадрат — рівнобічний прямокутник або ромб з прямими кутами при вершинах.

Паралелограм є плоскою геометричною фігурою, його аналогом у тривимірному просторі є паралелепіпед.

Each 25 minute is one 'pomodoro', and it's a 25-minute focused work.
You can write the time of the start and progress on the task.

З історії паралелограма

Слово «паралелограм» перекладається як «паралельні лінії» (від грецьких слів Parallelos - паралельний і gramme - лінія), цей термін був введений Евклідом. У своїй книзі «Начала» Евкліда довів наступні властивості паралелограма: протилежні сторони і кути паралелограма рівні, а діагональ ділить його навпіл. Про точці перетину паралелограма Евклід не згадує. Тільки до кінця середніх століть була розроблена повна теорія паралелограмів І лише в XVII столітті в підручниках з'явилися теореми про параллелограммах, які доводяться за допомогою теореми Евкліда про властивості паралелограма.

Як знайти площу паралелограма

Площа паралелограма

Площа паралелограма дорівнює добутку його сторони на висоту, яка перпендикулярна до цієї сторони:

$S=DC \cdot h_{DC}=BC \cdot h_{BC}$

Також площа паралелограма рівна добутку двох його непаралельних сторін та синуса кута між ними:

$S=DC \cdot AD \cdot \sin \angle D=DC \cdot BC \cdot \sin \angle C.$

Властивості паралелограма

Протилежні сторони паралелограма рівні, тобто $AB=DC$ та $AD=BC$ .
Протилежні кути паралелограма рівні, тобто $\angle A=\angle C$ та $\angle B=\angle D$ .
Діагоналі паралелограма перетинаються та точкою перетину діляться навпіл.
Точка перетину діагоналей є центром симетрії паралелограма.
Сума кутів, прилеглих до однієї сторони, дорівнює $180^\circ$ . Загальна сума кутів паралелограма дорівнює $360^\circ$ .
Паралелограм діагоналлю ділиться на два рівні трикутники.
Сума квадратів діагоналей дорівнює подвоєнній сумі квадратів двох його суміжних сторін (правило паралелограма).

Ромб

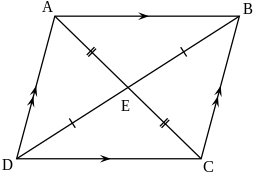
Ромб — паралелограм, усі сторони якого рівні.

Властивості ромба

Кожен ромб має дві діагоналі, що з'єднують пари протилежних вершин, і має дві пари паралельних сторін.

Це паралелограм, діагоналі якого розділяють внутрішній кут.

Протилежні кути ромба рівні.
Діагоналі ромба перетинаються під прямим кутом, точка перетину є серединою кожної діагоналі.
Діагоналі ромба є бісектрисами кутів, з яких вони проведені.
Сторони ромба попарно паралельні.
Точка перетину діагоналей називається центром симетрії ромба.
В будь-який ромб можна вписати коло.
Центром кола, вписаного в ромб, є точка перетину його діагоналей.
Сума квадратів діагоналей дорівнює квадрату сторони, помноженому на чотири: AC² + BD² = 4AB²

Однією з основних властивостей є те, що ромб - це паралелограм, внаслідок чого ромб має усі ті властивості, що й паралелограм. Наприклад,

протилежні сторони паралельні;

прилеглі кути є суміжними;

дві діагоналі поділяють одна одну навпіл;
будь-яка пряма, що проходить через центр, поділяє площу навпіл;

сума квадратів сторін дорівнює сумі квадратів діагоналей (правило паралелограма).

Отож, якщо позначити сторону як a, а діагоналі як d₁ і d₂, то для кожного ромба $\displaystyle 4a^{2}=d_{1}^{2}+d_{2}^{2}.$

Не кожен паралелограм є ромбом, але кожен паралелограм, у якого діагоналі є перпендикулярними, є ромбом. В загальному випадку будь-який чотирикутник з перпендикулярними діагоналями, одна з яких є лінією симетрії, - це дельтоїд.

How many Pomodoros you might need? Plan your pomodoros, then choose the task you want to start it with!

Ромб у вишивці

Ромб на вишиванці

Основні значення: союз сонця і землі, плодючість.

Ромб пов'язують із плодючістю людини і землі. Він складається із двох трикутників, які символізують чоловіче і жіноче начало. Ромб із крапкою посередині означає засіяне поле, яке для наших предків дорівнювало добробуту і достатку. Ромбоподібні узори вишивали на весільних рушниках та на весільному одязі молодої. Одяг із вишитими ромбами молода жінка, завагітнівши, мала носити аж до народження дитини.

Нарисуємо ромб разом!

Історична довідка

Слово «ромб» походить від грец. ῥόμβος (ромбос), що означає щось, що обертається, утворене своєю чергою від дієслова ῥέμβω (рембо), що означає «обертаюся довкола».

Слово використовувалося Евклідом і Архімедом, які використовували термін «об'ємний суцільний ромб» для двох круглих конусів зі спільною основою.

Та плоска фігура, яку ми сьогодні називаємо ромбом, є поздовжнім перетином того суцільного ромба, що проходить крізь вершини кожного з двох конусів.

Choose the task you want to start it with!

Чотирикутники

Ламана Многокутник і його елементи Сума опуклих кутів многокутника

Площі фігур

Площадь

Логотип бренду одягу