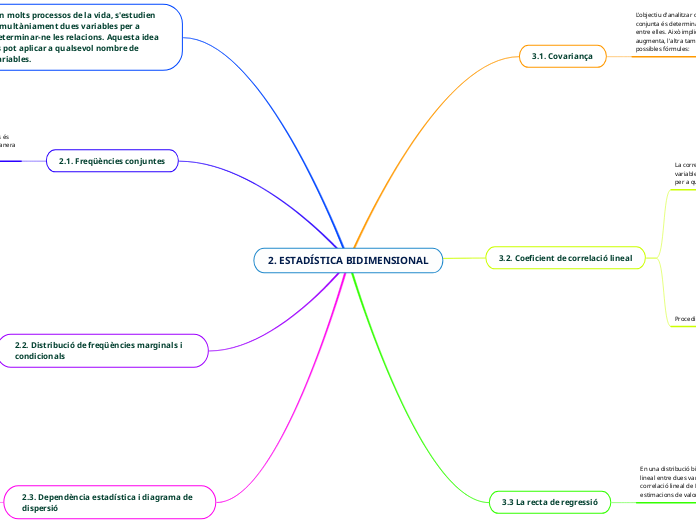
2. ESTADÍSTICA BIDIMENSIONAL

Mere som dette

M4 RETOS DE LA DEFENSA JURÍDICA DEL ESTADO ANTE LOS MEDIOS DE PRUEBA DIGITAL EN EL DERECHO CONTENCIOSO ADMINISTRATIVO COLOMBIANO

af UNIVERSIDAD SERGIO ARBOLEDA

mapa conceptual protocolo TCP/IP

af walther sanchez arango

EL PLAN DE INVESTIGACIÓN. ELEMENTOS BÁSICOS Y FORMAS DE PRESENTACIÓN.

af roberto venero

ÉTICA Y COMUNICACIÓN

af Kevin Pava

2. ESTADÍSTICA BIDIMENSIONAL

2.3. Dependència estadística i diagrama de dispersió

La dependència estadística és la relació entre dues variables, encara que no sigui exacta. Pot prendre formes com quadràtica, exponencial, lineal o funcional.

La regressió és l'estudi de la dependència estadística entre variables quantitatives, mentre que la correlació és l'anàlisi del grau de dependència entre aquestes variables. L'objectiu principal de la regressió és descobrir la forma en què es relacionen.

El núvol de punts o diagrama de dispersió és un gràfic utilitzat per a detectar relacions de dependència entre dues variables. Es representa els parells de valors en uns eixos de coordenades, amb la variable independent a l'eix X i la variable dependent a l'eix Y. Aquesta representació visual permet identificar possibles correlacions o tendències entre les variables.

2.2. Distribució de freqüències marginals i condicionals

Les distribucions condicionades es deriven de la distribució conjunta de freqüències. Es tracta de distribucions unidimensionals per a les variables X i Y, que s'obtenen fixant el valor de l'una mentre s'analitza la distribució de l'altra.

Freqüències relatives condicionades

per a Y (yj) atès que X (xi) és el nombre de vegades que es repeteix el valor ij tenint en compte només aquells valors en què X (xi

n(i)  j = nij per a tot j = 1, 2,..., h.

Freqüència absoluta condicionada

Per a X(xi) atès que Y(yj) és el nombre de vegades que es repeteix el valor xi tenint en compte només aquells valors en què Y (ij)

ni (j) = nij per a tot i = 1, 2, ..., k

Per distingir les freqüències individuals de cada variable, les anomenarem freqüències marginals. Això ens permetrà obtenir dues distribucions unidimensionals a partir de les distribucions conjuntes.

Freqüències relatives marginals

A partir de les anteriors, i de la mateixa manera, es construiran aquestes freqüències (fi) i (fj)

Freqüència absoluta marginal

Per la Y (yj) sería el número de vegades que es repeteix el valor yj sense tenir en compte els valors de la X, la representem per nj.

Per la X (xi) sería el número de vegades que es repeteix el valor xi sense tenir en compte els valors de la Y, la representem per ni

2.1. Freqüències conjuntes

Per descriure dues variables conjuntament, el primer pas és representar les dades en una taula de freqüències, de manera similar com es fa amb una única variable.

Taula de doble entrada

Es comú utilitzar una taula de contingència per a mostrar els valors d'una distribució estadística bidimensional. En aquesta taula, es registren els resultats d'una variable a la part superior i els valors de l'altra variable a l'esquerra. A cada casella de la taula s'indiquen les freqüències absolutes, relatives o percentatges de les dues variables.

Freqüència relativa conjunta (fij)

Fórmula: nij / n

Freqüència absoluta conjunta (nij)

Aquesta frase indica el nombre de vegades que es troba el valor xi de la variable X en la mostra, en relació amb el valor yj de la variable Y.

Propietat: la suma de les freqüències absolutes és igual a n.

En molts processos de la vida, s'estudien simultàniament dues variables per a determinar-ne les relacions. Aquesta idea es pot aplicar a qualsevol nombre de variables.

3.3 La recta de regressió

En una distribució bidimensional, si s'observa una correlació lineal entre dues variables, es pot utilitzar el coeficient de correlació lineal de Pearson (r) per fer prediccions o estimacions de valors possibles d'una variable.

Per realitzar aquestes prediccions, és necessari calcular una recta de regressió, la qual consisteix en trobar l'equació algebraica de la recta que millor s'ajusti al conjunt de punts de dades.

Hi ha dues rectes de regressió que es calcularan en funció de la correlació i les mitjanes i variàncies de les variables marginals:

La selecció de la recta a utilitzar depèn del context del problema. En alguns casos, l'enunciat ja indica quina recta s'ha d'utilitzar, mentre que en altres casos cal deduir-ho a partir de les dades.

La recta de regressió és aquella que millor s'ajusta a la distribució de punts (núvol de punts).

Si es demana predir el valor de x coneixent la corresponent y, s'ha d'utilitzar la recta de regressió de X sobre Y, ja que aïlla la variable X.

Si es demana predir un valor de y donat un valor de x, s'ha d'utilitzar la recta de Y sobre X, ja que aquesta recta aïlla la variable Y.

La de X sobre Y

X = x + (oxy/oy2) * (yj-y)

La  de Y sobre X

Y = y + (oxy/ox2) * (xi-x)

3.2. Coeficient de correlació lineal

Procediment

4. Amb l'ajuda d'aquestes taules i la suma total de les seves columnes es pot calcular tots els paràmetres

Coeficient de correlació lineal de Pearson

Covariància

Mitjana, variància i desviació típica d'X i d'Y

3. A partir d'aquesta taula crear 3 taules més

La tercera és la de la variable bidimensional XY

A les columnes hi situarem els valors (xi,yj), nij, xi * yj * nij

La segona és la de la variable Y

A les columnes hi situarem yj, yj * nj, yj2 * nj

La primera és la de la variable X

A les columnes hi situarem xi, xi * ni, xi2 * ni

2. Fer la taula de doble entrada

1. Saber quina és la variable X, i quina és la Y

La correlació és una mesura de la dependència entre dues variables. El coeficient de correlació de Pearson (r) és utilitzat per a quantificar aquesta correlació.

rxy = oxy / ox * oy

oy = arrel quadrada de ((sumatori de yi al quadrat * ni) / N - y al quadrat

y = mitjana de totes les yi

ox = arrel quadrada de ((sumatori de xi al quadrat * ni) / N - x al quadrat

x = mitjana de totes les xi

N = número total d'individus estudiats

oxy és la covariància

3.1. Covariança

L'objectiu d'analitzar dues variables quantitatives de manera conjunta és determinar si hi ha alguna relació o covariància entre elles. Això implica verificar si, quan una variable augmenta, l'altra també ho fa o viceversa. Hi han dues possibles fórmules:

Què ens indica el valor de la covariància entre dues variables?

Si oxy = 0

No hi ha dependència lineal

Si oxy < 0

Dependència lineal negativa

Si oxy > 0

Dependència lineal positiva

oxy = (sumatori (xi-x) * (yi-y)) / N

oxy = ((sumatori de xi*yi*ni)/N ) - (x*y)