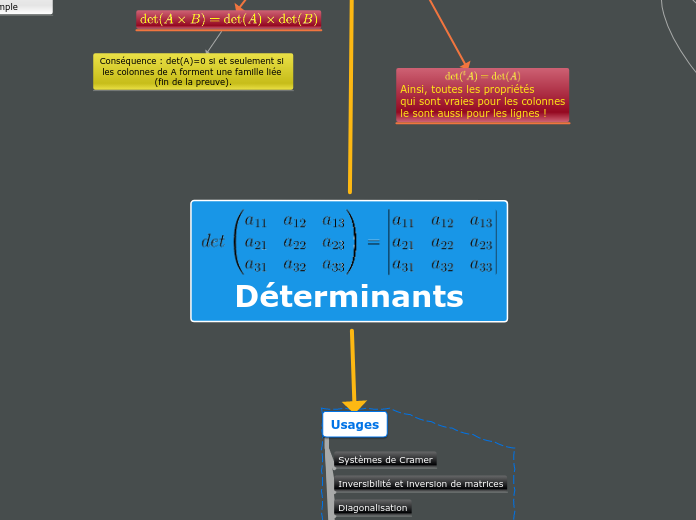
Déterminants
Calculs
Formule de développement selon une ligne
Matrice « damier »
Développement selon la ligne n°i
(rare dans les calculs)
Rem : si i=1, c'est la formule de
récurrence de la définition
Multilinéarité
Rem : si toutes les colonnes sont dilatées
Cas général d'une combi. linéaire
(rare dans les calculs)
Effet dilatation d'une colonne
Ainsi, toutes les propriétés
qui sont vraies pour les colonnes
le sont aussi pour les lignes !
Alternée
Si on échange deux colonnes, le dét change de signe
Conséquence 2 : det(A)=0 si et
seulement si les colonnes de A
forment une famille liée.
(début preuve)
donc matrice inversible
Conséquence 1 : on ne change pas la
valeur du dét si on ajoute à une col.
un multiple d'une autre.
Matrices particulières
Matrices triangulaires par blocs
(A et B sont carrées !)
Exemple
Matrices diagonales
Matrices triangulaires
Usages
Déterminants de familles de vecteurs
(lien avec les bases)
Déterminants d'endomorphismes
(lien avec les automorphismes)
Calculs d'hypervolumes
Diagonalisation
Inversibilité et inversion de matrices
Systèmes de Cramer