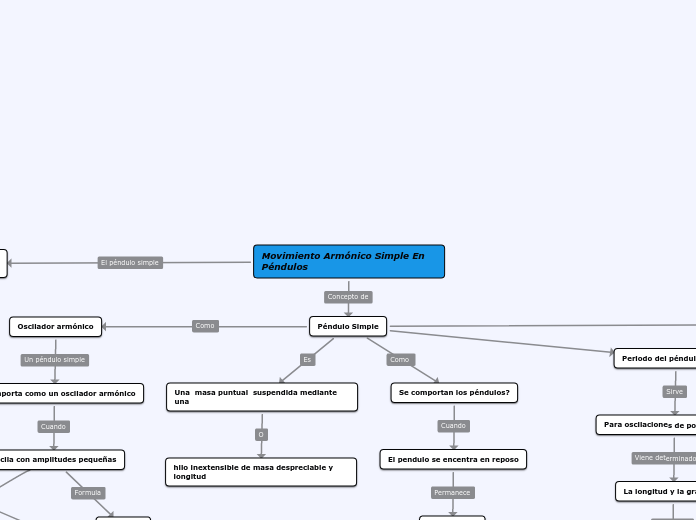
Movimiento Armónico Simple En Péndulos

Mere som dette

EL MOVIMIENTO DE LOS SATÉLITES

af VÍCTOR CHARRO BLANCO

Cuerpos celestes

af miguel men

FUERZA MUSCULAR

af Valentina Alzate Roa

SISTEMA ESTOMATOGNATICO

af german perez contreras

g: Gravedad

El metro por segundo al cuadrado (m/s2)

T: Periodo del péndulo

El segundo (s)

Donde:

x: Separación x de la vertical de equilibrio del péndulo

l: Longitud del péndulo

Es el metro (m)

g: Aceleración de la gravedad

Es 9.8 m/s2

a: Aceleración del péndulo

De la distancia a la posición de equilibrio x. (m/s2)

Movimiento Armónico Simple En Péndulos

Péndulo Simple

Periodo del péndulo simple

El tiempo que tarda el péndulo en volver a pasar por un punto en el mismo sentido

T=2⋅pi⋅√l/g

Para oscilaciones de poca amplitud,

La longitud y la gravedad

La masa de del cuerpo que oscila ni la amplitud de la oscilación

Oscilador armónico

Se comporta como un oscilador armónico

Oscila con amplitudes pequeñas

a=−g/l*x

Componentes tangencial y normal de una fuerza

el componente normal

La proyección de la fuerza sobre el eje normal

El componente tangencial

La proyección de la fuerza sobre el eje tangente

Se comportan los péndulos?

El pendulo se encentra en reposo

En Equilibrio

La fuerza peso

Por la tensión en la cuerda

Pn+T=O;Pt=-m*g*sin(α)

Una masa puntual suspendida mediante una

hilo inextensible de masa despreciable y longitud

Se puede considerar un caso de movimiento armónico simple

Se cumplen ciertas condiciones