Trabajo de Calculo.

Mere som dette

Mestizos

af Francis Silva

Secciones y Cortes

af Julian Corredor

Nuevo mapa

af Hedy Norma Flores Cabezas

El Municipio

af Fatima Gutiérrez

Hiperboloide, Polinomio en matemáticas y Interpolación polinomica

Interpolación polinomica

En análisis numérico, la interpolación polinómica (o polinomial) es una técnica de interpolación de un conjunto de datos o de una función por un polinomio. Es decir, dado cierto número de puntos obtenidos por muestreo o a partir de un experimento se pretende encontrar un polinomio que pase por todos los puntos.

Polinomio en matemáticas

Un polinomio es una expresión algebraica de sumas, restas y multiplicaciones ordenadas hecha de variables, constantes y exponentes. En álgebra, un polinomio puede tener más de una variable (x, y, z), constantes (números enteros o fracciones) y exponentes (que solo pueden ser números positivos enteros). Los polinomios están formados por términos finitos. Cada término es una expresión que contiene uno o más de los tres elementos de los que están hechos: variables, constantes o exponentes. Por ejemplo: 9, 9x, 9xy son todos términos. Otra forma de identificar los términos es que se separan por sumas y restas.

La cantidad de términos que un polinomio tiene indicará qué tipo de polinomio es, por ejemplo, Polinomio de un término: monomio, por ejemplo, 8xy. Polinomio de dos términos: binomio, por ejemplo, 8xy - 2y. Polinomio de tres términos: trinomio, por ejemplo, 8xy - 2y + 4.

hiperboloide

es la superficie de revolución generada por la rotación de una hipérbola alrededor de uno de sus dos ejes de simetría. Dependiendo del eje elegido, el hiperboloide puede ser de una o dos hojas. Para entenderlo mejor, se considera a continuación el caso de la hipérbola de referencia, cuya ecuación es

Superficie, Espacio,y Elipsoide

Espacio

Al hablar de geometría hasta ahora siempre lo hemos hecho, y sobre todo pensado, en dos dimensiones. Esto ya que es lo más fácil, tanto para su comprensión como para su estudio y representación. Pero, ahora aprenderemos un poco acerca del espacio como en verdad está hecho en tres dimensiones: el largo, el ancho y la longitud. Para poder hacerlo tendremos que usar mucho nuestras capacidades cerebrales imaginativas. Y nos ayudaremos sobre todo de graficadores para dispositivos electrónicos. Primeramente tenemos que hablar sobre el origen de las tres dimensiones.

Superficie

Para calcular la superficie, es el contorno de la figura, hay que sumar sus lados. Para el area hay que multiplicar los lados, en algunos casos como el triangulo es (base x altura)/2. El área de superficie total de un sólido es la suma de las áreas de todas las caras o superficies que encierran el sólido.

Elipsoide

Un elipsoide es una superficie curva cerrada cuyas tres secciones ortogonales principales son elípticas, es decir, son originadas por planos que contienen dos ejes cartesianos cada plano. En matemática, es una cuádrica análoga a la elipse, pero en tres dimensiones. Un elipsoide se obtiene al «deformar» una esfera, mediante una transformación homológica, en la dirección de sus tres diámetros ortogonales. Al rotar una elipse alrededor de uno de sus dos ejes se obtiene un elipsoide de revolución o esferoide.

La ecuación de un elipsoide con centro en el origen de coordenadas y ejes coincidentes con los cartesianos, es:

donde a, b y c son las longitudes de los semiejes del elipsoide respecto de los ejes x, y, z, respectivamente; son números reales positivos y determinan la forma del elipsoide. Si dos de estos semiejes son iguales, el elipsoide es un esferoide; si los tres son iguales, se trata de una esfera.

Producto vectorial de dos vectores y Producto escalar

Producto vectorial de dos vectores btopic

La magnitud del producto vectorial de dos vectores es el resultado de multiplicar las magnitudes de cada vector y por el seno del ángulo que forman ambos vectores (< 180 grados) entre ellos.

Subtopic

Producto Escalar

En matemáticas, el producto escalar, también conocido como producto interno o producto punto, es una operación algebraica que toma dos secuencias de números de igual longitud (usualmente en la forma de vectores) y retorna un único número. Algebraicamente, el producto punto es la suma de los productos de las correspondientes entradas en dos secuencias de números. Geométricamente, es el producto de dos magnitudes euclidianas de los dos vectores y el coseno del ángulo entre ellos. El nombre del producto punto se deriva del símbolo que se utiliza para denotar esta operación (« · »). El nombre alternativo de producto escalar enfatiza el hecho de que el resultado es un escalar en lugar de un vector (en el caso de espacios de tres dimensiones)

Aproximación, sistema de ecuaciones, método de biseccion, posición falsa, Newton Raphson

Aproximacion inicial y criterios de convergencia

En los metodos que parten de un intervalo [a,b] en el que la funcion cambia de signo, no importa lo grande que este sea, se tiene la seguridad de que habra convergencia a una raiz. Por esta razon se denominan globalmente convergentes. Sin embargo si en [a,b] hay varias raices sera necesario determinar intervalos mas pequenos para cada una de ellas, y esto no suele ser facil.

El metodo de Newton-Raphson

Si f(x), f '(x) y f ''(x) son continuas cerca de una raiz p de f, esta informaciÛn adicional sobre la naturaleza de f(x) puede usarse para desarrollar algoritmos que produzcan sucesiones {pk} que converjan a p mas rapidamente que en el metodo de biseccion o en el de la regula falsi. El metodo de Newton-Raphson, que descansa en la continuidad de f '(x) y f ''(x), es uno de los algoritmos mas utiles y mejor conocidos. Lo introduciremos graficamente y luego daremos un tratamiento mas riguroso basado en el teorema de Taylor.

Sistema de Ecuaciones

Un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas en la que deseamos encontrar una solución común. En esta ocasión vamos a resolver un sistema de dos ecuaciones lineales con dos incógnitas. Una ecuación lineal con dos incógnitas es una igualdad del tipo ax+by=c, donde a, b, y c son números, y «x» e «y» son las incógnitas. Una solución es todo par de números que cumple la ecuación. Los sistemas de ecuaciones lineales los podemos clasificar según su número de soluciones: Compatible determinado: Tiene una única solución, la representación son dos rectas que se cortan en un punto. Compatible indeterminado: Tiene infinitas soluciones, la representación son dos rectas que coinciden. Incompatible: No tiene solución, la representación son dos rectas paralelas.

El metodo de la falsa posicion (regula falsi)

Otro algoritmo popular es el mÈtodo de la regula falsi o metodo de la falsa posicion. Una de las razones de su introducciÛn es que la velocidad de convergencia del metodo de biseccion es bastante baja. Como antes, supongamos que f(a) y f(b) tienen distinto signo. Suele conseguirse un aproximaciÛn mejor que en el mÈtodo de la biseccion usando el punto (c,0) en el que la recta secante L que pasa por los puntos (a,f(a)) y (b,f(b)) cruza el eje OX

El metodo de la biseccion

El metodo comienza con un intervalo de partida [a,b] en el que f(a) y f(b) tienen distinto signo. El metodo de biseccion consiste en ir acercando sistematicamente los extremos del intervalo hasta obtener un intervalo de anchura suficientemente pequena en el que se localiza un cero. El proceso de decision para subdividir el intervalo consiste en tomar el punto medio del intervalo c = (a+b)/2 y luego analizar las tres posibilidades que pueden darse: Si f(a) y f(c) tienen signos opuestos, entonces hay un cero en [a,c]. Si f(c) y f(b) tienen signos opuestos, entonces hay un cero en [c,b]. Si f(c) = 0, entonces c es un cero. Para continuar el proceso, renombramos el nuevo intervalo mas pequeno tambien como [a,b] y repetimos el proceso hasta que el intervalo sea tan pequeno como deseemos.

Error absoluto y error relativo porcentual y Errores de varias mediciones

Formula

Error Absoluto = Resultado Exacto – Aproximación.

Error Relativo = (Error Absoluto/ Resultado Exacto) x 100%

El tiempo que se calcula debe tardar una pelota en alcanzar el suelo después de ser lanzada a una distancia de 4 metros, es de 3 segundos. Sin embargo, en el momento de la experimentación, se descubre que la pelota tardó 2,1 segundo el alcanzar el suelo. Ea = 3 – 2,1 Ea = 0,9 segundos Ep = (0,9/2,1) x 100 Ep = 42,8%

Se asumió que 1,000,000 de personas irían a un evento determinado. Sin embargo, el número exacto de personas que fue a dicho evento fue de 88,000. El error absoluto y porcentual serían los siguientes: Ea = 1,000,000 – 88,000 Ea = 912,000 Ep = (912,000/1,000,000) x 100 Ep = 91,2%

Toda medida debe de ir seguida por la unidad, obligatoriamente del Sistema Internacional de Unidades de medida. Cuando un físico mide algo debe tener gran cuidado para no producir una perturbación en el sistema que está bajo observación. Por ejemplo, cuando medimos la temperatura de un cuerpo, lo ponemos en contacto con un termómetro. Pero cuando los ponemos juntos, algo de energía o "calor" se intercambia entre el cuerpo y el termómetro, dando como resultado un pequeño cambio en la temperatura del cuerpo que deseamos medir. Así, el instrumento de medida afecta de algún modo a la cantidad que deseábamos medir Además, todas las medidas está afectadas en algún grado por un error experimental debido a las imperfecciones inevitables del instrumento de medida, o las limitaciones impuestas por nuestros sentidos que deben de registrar la información.

El error absoluto se define como la diferencia entre el valor real y el valor aproximado, en valor absoluto El valor real es el valor que en teoría mide la magnitud a medir El valor aproximado es la media de las diferentes medidas Este valor del error absoluto es el debido a la persona que realiza la medición. Además, está el error debido a la precisión del instrumento de medida, que coincide con la unidad más pequeña con la que puede medir el aparato. El error absoluto será el mayor valor entre el error del medidor y el error del aparato. El error absoluto se mide en las mismas unidades que la medición.

El error porcentual es la manifestación de un error relativo en términos porcentuales. En otras palabras, es un error numérico expresado por el valor que arroja un error relativo, posteriormente multiplicado por 100. Error Relativo = (Error Absoluto/ Resultado Exacto) x 100%

Cifras significativas

Para distinguir los llamados significativos de los que no son, estos últimos suelen indicarse como potencias por ejemplo 5000 será 5x103 con una cifra significativa. También, cuando una medida debe expresarse con determinado número de cifras significativas y se tienen más cifras, deben seguirse las siguientes reglas:

Primera: si se necesita expresar una medida con tres cifras significativas, a la tercera cifra se le incrementa un número si el que le sigue es mayor que 5 o si es 5 seguido de otras cifras diferentes de cero. Ejemplo: 53,6501 consta de 6 cifras y para escribirlo con 3 queda 53,7; aunque al 5 le sigue un cero, luego sigue un 1 por lo que no se puede considerar que al 5 le siga cero (01 no es igual a 0).

Segunda: siguiendo el mismo ejemplo de tres cifras significativas: si la cuarta cifra es menor de 5, el tercer dígito se deja igual. Ejemplo: 53,649 consta de cinco cifras, como se necesitan 3 el 6 queda igual ya que la cifra que le sigue es menor de 5; por lo que queda 53,6.

Tercera: cuando a la cifra a redondear le sigue un 5 , siempre se redondea hacia arriba. Ejemplo: si el número es 3,7500 se redondearía a 3,8.2

Son significativos todos los dígitos distintos de cero. Los ceros situados entre dos cifras significativas son significativos. Los ceros a la izquierda de la primera cifra significativa no lo son. Para números mayores que 1, los ceros a la derecha de la coma son significativos. Para números sin coma decimal, los ceros posteriores a la última cifra distinta de cero pueden o no considerarse significativos. Así, para el número 70 podríamos considerar una o dos cifras significativas. Esta ambigüedad se evita utilizando la notación científica.

8723 tiene cuatro cifras significativas

105 tiene tres cifras significativas

0,005 tiene una cifra significativa

8,00 tiene tres cifras significativas

7 · 102 tiene una cifra significativa 7,0 · 102 tiene dos cifras significativas

Las cifras significativas de una medida son las que aportan alguna información.1 Representan el uso de una o más escalas de incertidumbre en determinadas aproximaciones. Por ejemplo, se dice que 4,7 tiene dos cifras significativas, mientras que 4,07 tiene tres.

Medida de ángulo: sistema sexagesimal, centesimal y radianes.

La medida de un ángulo es considerada como la amplitud del arco de circunferencia centrada en el vértice y delimitada por sus lados. Su medida es un múltiplo de la razón entre la longitud del arco y el radio

Radianes

Dada una circunferencia de centro O y radio r, se denomina radian al ángulo central cuyo arco coincide con el radio.

Centesimal

La medida de ángulos centesimal se adopto con el sistema métrico decimal. El ángulo completo 360º en el sistema sexagesimal se divide en 400 partes iguales y un ángulo recto en 100, se notan por 100 g. Y le llama gradian. A su vez cada grado centesimal (gradian) se divide en 100 partes iguales que son los minutos, se nota por 1m y cada minuto se subdivide en 100 segundos que lo notaremos por 1s. Las operaciones son análogas a las sexagesimales pero más fáciles al usar un sistema de base 100.

Sis.Sexagesimal

La unidad de medida de ángulos del sistema sexagesimal es el grado (º), que es el resultado de dividir el ángulo llano en 180 partes iguales. Así, un ángulo recto mide 90º. Cada grado se divide en 60 minutos (´) y, cada minuto, en 60 segundos (´´).

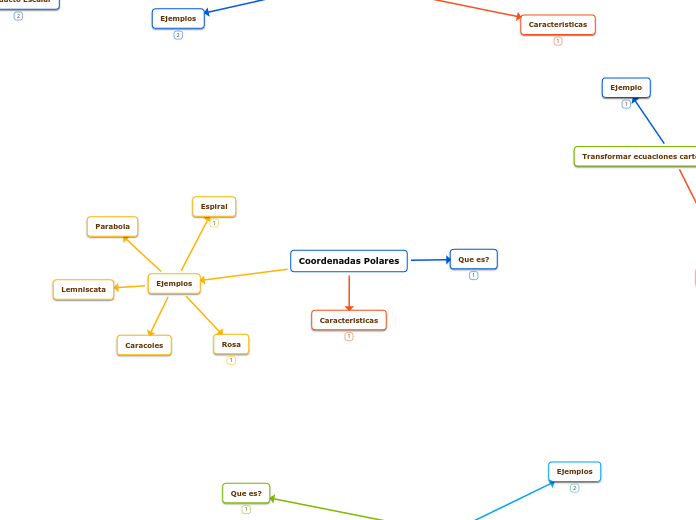
Transformar ecuaciones cartesianas a polares

Para transformar una ecuación en coordenadas cartesianas F( x, y)=0 a coordenadas polares F’( r, Ɵ) basta con hacer la sustitución en la ecuación original: x= r cos Ɵ y= r sen Ɵ

Las coordenadas polares de un punto del plano (r, Ɵ), se transforman en coordenadas cartesianas (x, y), mediante las siguientes ecuaciones:

Ejemplo

X^2+Y^2=16 x^2+Y^2-2x+y=9

Coordenadas cartesianas

Las coordenadas cartesianas o coordenadas rectangulares (sistema cartesiano) son un tipo de coordenadas ortogonales usadas en espacios euclídeos, para la representación gráfica de una relación matemática o del movimiento o posición en física, caracterizadas por tener como referencia ejes ortogonales entre sí que concurren en el punto de origen. En las coordenadas cartesianas se determinan las coordenadas al origen como la longitud de cada una de las proyecciones ortogonales de un punto dado sobre cada uno de los ejes. La denominación de 'cartesiano' se introdujo en honor de René Descartes, quien las utilizó por primera vez de manera formal.

El sistema en sí es un sistema bidimensional, que se denomina plano cartesiano. El punto de intersección de las rectas, por definición, se considera como el punto cero de las rectas y se conoce como origen de las coordenadas. Al eje horizontal o de las abscisas se le asigna los números reales de las equis ("x"); y al eje vertical o de las ordenadas se le asignan los números reales de las ye ("y"). Al cortarse las dos rectas, dividen al plano en cuatro regiones o zonas, que se conocen con el nombre de cuadrantes: Primer cuadrante "I": Región superior derecha Segundo cuadrante "II": Región superior izquierda Tercer cuadrante "III": Región inferior izquierda Cuarto cuadrante "IV": Región inferior derecha

Coordenadas Polares

Ejemplos

Espiral

La espiral de Arquímedes es una famosa espiral descubierta por Arquímedes, la cual puede expresarse también como una ecuación polar simple.

Lemniscata

Rosa

La rosa polar es una famosa curva matemática que parece una flor con pétalos, y puede expresarse como una ecuación polar simple.

Parabola

Caracoles

Caracteristicas

Si se elije en el plano un punto O (Polo) y una recta o eje polar, que tiene su origen en el punto O. La posición de un punto en el plano se representa por dos números: ρ y φ. El primero indica la distancia del punto M al Polo, y el segundo, el valor del ángulo formado por el segmento OM con el eje polar. Para calcular el ángulo φ se considera positiva la dirección contraria a las manecillas del reloj. Los números ρ y φ se denominan coordenadas polares del punto M. El radio vector ρ se considera siempre no negativo, si el ángulo polar φ en los límites de 0 ≤ φ≤ 2π, a cada punto del plano a acepción del Polo le corresponde un par de valores ρ y φ. En el polo ρ = 0 y φ puede tener cualquier valor.

Que es?

El sistema de coordenadas polares es un sistema de coordenadas bidimensional en el cual cada punto del plano se determina por un ángulo y una distancia. ... La distancia se conoce como la coordenada radial o radio vector, mientras que el ángulo es la coordenada angular o ángulo polar