Трикутники
Трикутником називається геометрична фігура на площині, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які попарно сполучають ці точки. Точки називаються вершинами трикутника, а відрізки - сторонами трикутника.
Рівність трикутників
Трикутники називаються рів& ними, якщо у них відповідні сто& рони і кути рівні ∆АВС = ∆А′В′С′
Властивості рівних трикутників
У рівних трикутників усі відповідні елементи рівні (сторони, кути, висоти, медіани, бісектриси). У рівних трикутників проти рівних сторін лежать рівні кути, а проти рівних кутів лежать рівні сторони.
Ознаки рівності трикутників
І ознака (за двома сторонами і кутом між ними
Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники є рівними.
ІІ ознака (за стороною і прилеглими кутами)
Якщо сторона і два прилеглі до неї кути одного трикутника відповідно дорівнюють стороні і двом прилеглим до неї кутам другого трикутника, то такі трикутники - рівні.
ІІІ ознака (за трьома сторонами)
Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам другого трикутника, то такі трикутники є рівними.
Подібність трикутників
Подібними називаються трикутники, у яких відповідні сторони пропорційні. Коефіцієнт пропорційності називається коефіцієнтом подібності
Властивості подібних трикутників
У подібних трикутників відповідні кути рівні, а відповідні відрізки пропорційні ∠А = ∠А'; ∠В = ∠В'; ∠С = ∠С'; ha/ha'=hb/hb'=hc/hc'=ma/ma'=...=lc/lc'=k.Відношення периметрів подібних трикутників дорівнює коефіцієнту подібності.Відношення площ подібних трикутників дорівнює квадрату коефіцієнта подібності.Якщо ΔABC ~ ΔА1В1С1, тоПряма, що паралельна одній із сторін трикутника, відсікає трикутник, подібний до даного KL | | AC; ∆ABC ~ ∆ KBLТри середні лінії трикутника ділять його на чотири рівні трикутники, подібні до даного з коефіцієнтом подібності 1/2.
Ознаки подібності трикутників
І ознака
Якщо два кути одного трикутника відповідно дорівнюють двом кутам іншого, то такі трикутники подібні.Якщо ∠B=∠E і ∠C=∠F, тоді ΔABC∼ΔDEF.
ІІ ознака
Якщо дві сторони одного трикутника пропорційні двом сторонам іншого трикутника і кути, утворені цими сторонами рівні, то такі трикутники подібні. ΔABC∼ΔDEF.
ІІІ ознака
Якщо три сторони одного трикутника пропорційні трьом сторонам іншого, то такі трикутники подібні.
Теорема косинусів
Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.
Теорема синусів
Сторони трикутника пропорційні до синусів протилежних кутів.
Властивості кутів і сторін
Сума кутів трикутника
Сума кутів трикутника дорівнює 180°α + β + γ = 180°
Зовнішній кут
Важливими є наступні властивості зовнішнього кута трикутника.1. Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних з ним.На малюнку 215: ∠ВАК = ∠B + ∠C.2. Зовнішній кут трикутника більший від будь-якого внутрішнього кута, не суміжного з ним.На малюнку 215: ∠ВАК > ∠С; ∠ВАК >∠В.3. Сума зовнішніх кутів трикутника, взятих по одному при кожній вершині, для будь-якого трикутника дорівнює 360°. На малюнку 216: 1 + 2 + 3 = 360°.
Нерівність трикутника
Довжина кожної сторони менша, ніж сума, і більша, ніж різниця довжин двох інших сторін| a − b | < c < a+b
Сторона і протилежний кут
У трикутнику проти більшої сторони лежить більший кут (і навпаки)∠B > ∠C ⇒ b > c
Площа
Медіани, бісектриси, висоти і середні лінії трикутника
Висота
Висотою трикутника, опущеною з даної вершини, називається перпендикуляр, проведений з цієї вершини до прямої, що містить протилежну сторону трикутника.Довжину висоти трикутника, яка проведена до сторони a, можна знайти за формулою:
Медіана
Медіаною трикутника називається відрізок прямої, що з’єднує вершину трикутника з серединою протилежної сторони.Властивості:Три медіани трикутника перетинаються в одній точці, що ділить медіани у відношенні 2 : 1, рахуючи від вершини. ВЕ : ЕМ = 2.Медіани ділять трикутник на рівновеликі трикутники S∆АВК=S∆КВС.Довжину медіани трикутника, яка проведена до сторони a, можна знайти за формулою
Бісектриса
Бісектрисою трикутника називається відрізок бісектриси внутрішнього кута трикутника, що з’єднує дану вершину з точкою на протилежній стороні.Властивості:Бісектриси внутрішніх кутів трикутника перетинаються в одній точці, що знаходиться всередині трикутника, рівновіддалена від трьох його сторін і є центром вписаного кола.Бісектриса внутрішнього кута трикутника ділить протилежну куту сторону на відрізки, пропорційні двом іншим сторонам AD/DC=AB/BC.Бісектриси внутрішнього і суміжного з ним зовнішнього кутів перпендикулярні. Бісектриса зовнішнього кута трикутника ділить (зовнішньо) протилежну сторону на відрізки, пропорційні двом іншим сторонам. BD — бісектриса кута В; ВЕ — бісектриса зовнішнього кута ВD ⊥ BE; AE/CE=AB/BC.Довжину бісектриси трикутника, яка проведена до сторони a, можна знайти за формулою
Середня лінія трикутника
Середньою лінією трикутника називається відрізок, що з’єднує середини двох сторін трикутник.Середня лінія трикутника паралельна одній із його сторін і дорівнює половині цієї сторони.EF∥ACEF=AC/2
Види трикутників
За кутами

Тупокутний
Якщо один із кутів трикутника є тупим, то трикутник називається тупокутним.

Госторокутний
Якщо всі кути трикутника є гострими, то трикутник називається гострокутним.

Прямокутний
Трикутник називається прямокутним, якщо один з його кутів прямий.
Ознаки рівності
1.Ознака рівності за двома катетами: якщо катети одного прямокутного трикутника дорівнюють катетам іншого, то такі трикутники рівні.2.Якщо катет і прилеглий до нього гострий кут одногопрямокутного трикутника дорівнюють катету та прилеглому до нього гострому куту іншого, то такі трикутники рівні.3.Якщо гіпотенуза й гострий кут одного прямокутного трикутника дорівнюють гіпотенузі та гострому куту іншого, то такі трикутники рівні.4.Якщо гіпотенуза й катет одного прямокутного трикутника дорівнюють гіпотенузі й катету іншого, то такі трикутники рівні.
Ознаки подібності
За гострим кутом. Якщо прямокутні трикутники мають по рівному гострому куту, то такі трикутники подібні. У прямокутного трикутника один кут прямий, тому для подібності двох прямокутних трикутників досить, щоб у них було по рівному гострому куту.За двома пропорційними катетами. Якщо катети одного прямокутного трикутника пропорційні катетам другого прямокутного трикутника, то такі трикутники подібні. За пропорційними катетом і гіпотенузою. Якщо катет і гіпотенуза одного прямокутного трикутника пропорційні катету і гіпотенузі другого прямокутного трикутника, то такі трикутники подібні.
Теорема Піфагора
У прямокутному трикутнику сума квадратів катетів дорівнює квадрату гіпотенузи.
Співвідношення між елементами сторін
прямокутного трикутника
Синусом гострого кута α прямокутного трикутника називають відношення катета, протилежного куту α, до гіпотенузи:. Косинусом гострого кута α прямокутного трикутника називають відношення катета, прилеглого до кута α, до гіпотенузи:. Тангенсом гострого кута α прямокутного трикутника називають відношення катета, прилеглого до кута α, до катета, протилежного куту α:. Котангенсом гострого кута α прямокутного трикутника називають відношення катета, прилеглого до кута α, до катета, протилежного куту α:.
Формули зв’язку між тригонометричними
функціями
Вписане коло
У прямокутний трикутник ABC з прямим кутом вписане коло, яке дотикається до катетів у точках і . Відрізки і дорівнюють радіусу кола.Радіус вписаного кола у прямокутний трикутник з катетами і і гіпотенузою знаходиться за формулою:
Описане коло
Центром кола, описаного навколо прямокутного трикутника, є середина гіпотенузи. Нехай — центр описаного кола навколо прямокутного ABC:
Площа прямокутного трикутника
Метричні співвідношення
Квадрат висоти прямокутного трикутника, проведеної до гіпотенузи, дорівнює добутку проекцій катетів на гіпотенузу.Квадрат катета дорівнює добутку гіпотенузи і проекції цього катета на гіпотенузу.
За сторонами
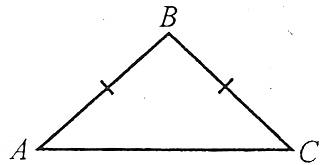
Рівнобедрений
Трикутник називається рівнобедреним, якщо в нього дві сторони рівні. Ці дві сторони називаються бічними сторонами, а третя сторона називається основою трикутника.
Властивості рівнобедреного трикутника
1.У рівнобедреному трикутнику кути при основі рівні ∠ А = ∠С.2.У рівнобедреному трикутнику медіана, проведена до основи, є бісектрисою і висотою BD — медіана, бісектриса, висота.Рівнобедрений трикутник має одну вісь симетрії.

Рівносторонній (правильний)
Трикутник називається правильним (рівностороннім), якщо в нього всі сторони рівні.
Властивості рівностороннього трикутника
У правильному трикутнику всі кути рівні 60°.У правильному трикутнику всі медіани є одночасно бісектрисами та висотами.Центри вписаного і описаного кіл збігаються

Різносторонній
Різностороннім називається трикутник, у якого всі сторони мають різну довжину. Внутрішні кути різностороннього трикутника різні.
Трикутник і коло
Вписане коло
Коло називається вписаним у трикутник, якщо воно дотикається до всіх його сторін.Точка перетину бісектрис трикутника є центром вписаного в нього кола.Радіус R вписаного кола можна обчислити за формулами: або ,де a, b, c – довжини сторін трикутника, – півпериметр трикутника, S – його площа.
Описане коло
Описаним колом трикутника називається коло, що проходить через вершини трикутника.Точка перетину серединних перпендикулярів трикутника є центром описаного навколо нього кола.Означення. Серединним перпендикуляром називається пряма, яка перпендикулярна до сторони та проходить через її середину.Радіус R описаного кола можна обчислити за формулами: або ,де a, b, c – довжини сторін трикутника, – півпериметр трикутника, S – його площа.