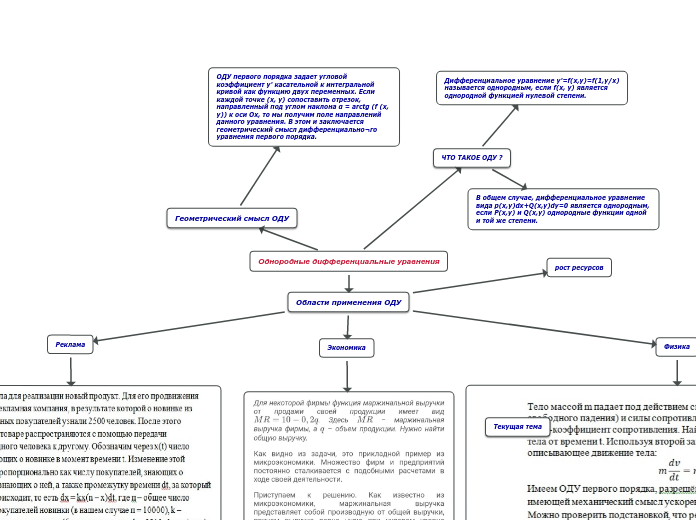
Однородные дифференциальные уравнения
ЧТО ТАКОЕ ОДУ ?
Дифференциальное уравнение y'=f(x,y)=f(1,y/x) называется однородным, если f(x, y) является однородной функцией нулевой степени.
В общем случае, дифференциальное уравнение вида p(x,y)dx+Q(x,y)dy=0 является однородным, если P(x,y) и Q(x,y) однородные функции одной и той же степени.
Геометрический смысл ОДУ
ОДУ первого порядка задает угловой коэффициент у' касательной к интегральной кривой как функцию двух переменных. Если каждой точке (x, у) сопоставить отрезок, направленный под углом наклона α = arctg (f (x, y)) к оси Ох, то мы получим поле направлений данного уравнения. В этом и заключается геометрический смысл дифференциально¬го уравнения первого порядка.
Области применения ОДУ
Экономика

Реклама

рост ресурсов
Физика