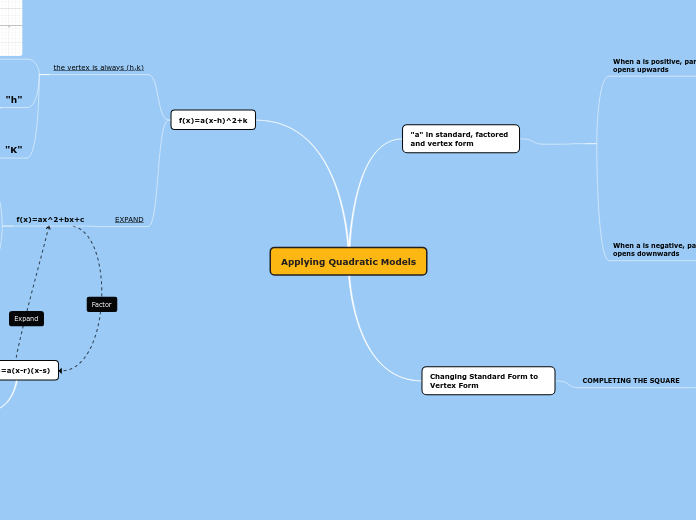
Applying Quadratic Models
"a" in standard, factored and vertex form
When a is positive, parabola opens upwards
a>1
blue parabola is y=x^2
red parabola is y=2x^2
Parabola is stretched vertically by a
factor of "a"
the greater the value of "a" the more stretched
0<a<1
blue parabola is y=x^2
red parabola is y=0.5x^2
Parabola is compressed vertically by
a factor of "a"
the greater the value of "a" the more compressed
When a is negative, parabola opens downwards
a<0
blue parabola is y=x^2
red parabola is y=-x^2
Parabola is reflected across the x axis
When "a" is negative and a>1
parabola is stretched then reflected
When "a" is negative and <a<1
parabola is compressed then reflected
Changing Standard Form to Vertex Form
COMPLETING THE SQUARE
Subtopic
f(x)=a(x-h)^2+k
the vertex is always (h,k)
"h"
the parabola moves "h" units left or right.
"h" is positive, parabola moves left
"h" is negative, parabola moves rigt
value of "h" is the axis of symmetry
"K"
the parabola moves "k" units up or down
EXPAND
f(x)=ax^2+bx+c
c is the "y intercept"
f(x)=a(x-r)(x-s)
roots (x intercepts) x=r and x=s
axis of symmetry = (r+s)/2
vertex= ( (r+s)/2 , y )