Chapter 4: Quadratic Relations

Simple Quadratics

Exponent or Power

A raised number to indicate repeated multiplication of a base number

Exponent Law

A set of rules that can be used to simplify powers

Expression

A mathematical phrase made up of numbers and variables,
connected by operators ( -, +)

Algebra

Distributive Property

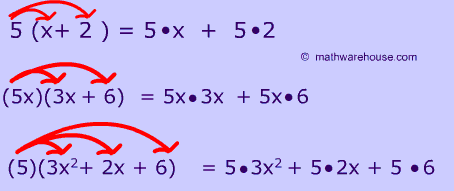
Variables

Strategies on Solving Word Problems

Find The Given.

Sketch a graph

Find the vertex,
value of 'a', direction of opening

1.Obtain info from the graph
2. Sketch important parts
with whatever information
you have
3. Understand

Formula: Y=x^2

Formula: Y=x^2

Subtopic

Multiply Polynomials

FOIL: (First, Outside, Inside, Last)

FOIL: (First, Outside, Inside, Last)

Quadratic Expression

A second degree polynomial

Ex: 4x^2+20 and x^2+7x+10 are quadratic expressions

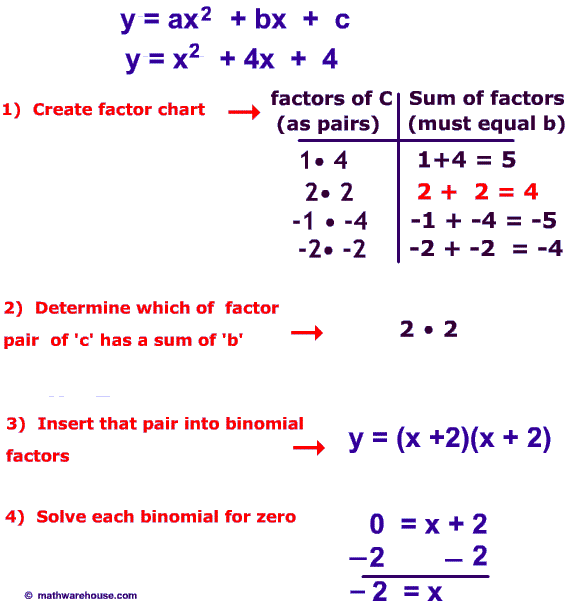
Special Products

Perfect square trinomial

Perfect square trinomial

Difference of squares

Difference of squares

Common Factors:

Common Factors:

Greatest common factors are used in factoring polynomial,
In fact factoring is the opposite of expanding

Quadratic Equations

3 possible outcomes

3 possible outcomes

Standard form

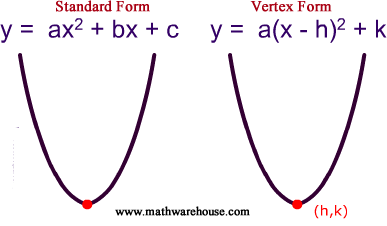
Standard form

What can we read: Direction of opening
and Y-intercept

Vertex form

Vertex form

What We Can Read: Vertex(h,k), Direction of opening,
The min/max value and AOS

Factored form

Factored form

What We Can Read: Direction of opening
and x-intercepts

Roots

Roots

also known ass x-intercepts or zeroes

Solving Quadratic Equations

graphing

Can be used always

factoring

Can be used sometimes/ use when C=0

C.T.S

Can be used always best when in standard form

quadratic formula

always best for precise roots

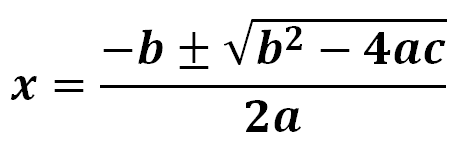
Quadratic Formula.

Quadratic Formula.

Used best for precise roots

- If b^2-4ac>0 = to 2 real roots

- If b^2-4ac<0 no real roots

- If b^2-4ac=0 ! real root or 2 equal roots

Completing the Square

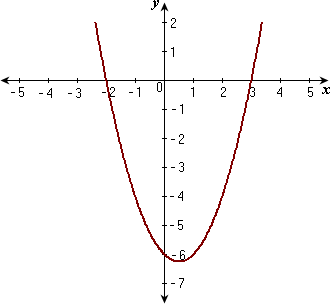
Parabolas

Standard and Vertex form equations

Standard and Vertex form equations

Subtopic

Non-Linear relations

Non-Linear relations

A curved line

Relation

An identified pattern between 2 variable

May be expressed in ordered pairs, a table of values, a graph, or an equation

STEP Method

How to do the step method:

1a, 3a, 5a, and 7a

Translation

Reflection

Reflection

A transformation in which a point and its image are equidistant from the line of reflection

Rotation

Rotation

A transformation of a geometric shape in which each point is turned about a centre point

Non Linear relations

x is the independent variable
to be solved 1st

y is the dependent variable
solved after x
affected by the independent variable (x)

Vertical Stretch and Compression

Vertical stretch
is 1<a<-1

Vertical compression
is -1<a<1

Some Key definitions

Some Key definitions

Vertex: A point at which the curve changes direction
Congruent: Equal size and shape
Parabola: a symmetrical open plane curve formed by the
intersection of a cone with a plane parallel to its side
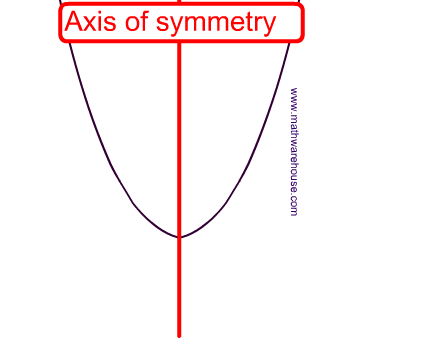
Axis of symmetry: Vertical line drawn through the vertex

Linear relations

Linear relations

Straight line

X- intercepts: The x-coordinates of the point where a line or curve crosses the y- axis, at this point y=0

y-intercepts: the y-coordinate of the point where a line or curve crosses the y- axis, at this point x is 0

Properties of a Parabola

Vertex, Axis of symmetry, Min/Max value, direction
of opening, Values 'x' may take, Values 'y' may take,
stretch or compression factor relative to y=x^2,
Congruent( = in size and shape)

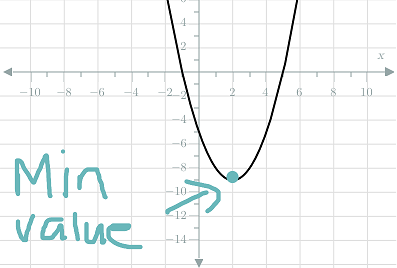
Minimum value occurs when parabola opens upwards

Minimum value occurs when parabola opens upwards

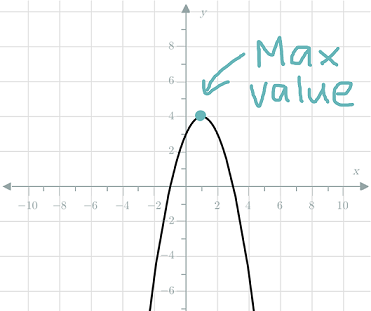
Maximum value occurs when parabola opens downwards

Maximum value occurs when parabola
opens downwards

Zeroes

A value of x which a relation has a value of 0

They correspond to the x- intercept of the graph of the relation

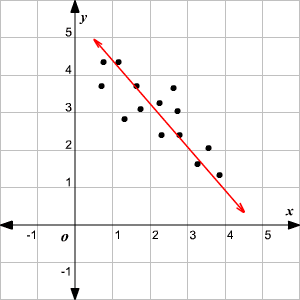
Line of best fit

Line of best fit

A straight line to best represent data or a trend in a scatter plot

Curve of best fit

Curve of best fit

A curved line to best represent data or a trend in a scatter plot

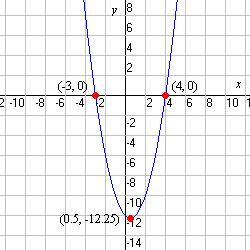
Mirror points

Mirror points

A point that is reflected in the axis of symmetry

Main topic

'a' value, 'k' value and 'h' value

The 'h' value controls the horizontal translation of the parabola (left and right)

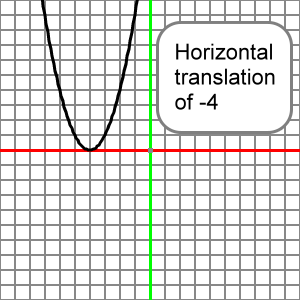
In this case the 'h' value was +4 and a horizontal translation of 4 to the left relative to y=x^2

In this case the 'h' value was +4 and
a horizontal translation of 4 to the left
relative to y=x^2

The 'k' value controls the vertical translation of the parabola (up and down)

In this case the 'k' value is -1 and the vertical translation was 1 down and horizontal translation was 3 to the right relat

In this case the 'k' value is -1 and the vertical translation
was 1 down and horizontal translation was 3 to the right relative to y=x^2

The 'a' value can cause a vertical stretch or compression, changing the direction of opening and shape of the curve and/or it can cause a reflection

Right here shows a vertical stretch by a factor of 3

Right here shows a vertical stretch by a factor of 3

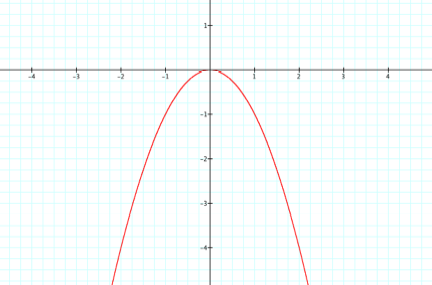
Reflection a<0

Reflection
a<0

Right here shows a vertical compression by a factor of 1/2

Right here shows a vertical compression by a
factor of 1/2

Quadratic Relations

a relation in the form of y = ax^2 + bx + c
a, b and c are real numbers and a can not equal zero

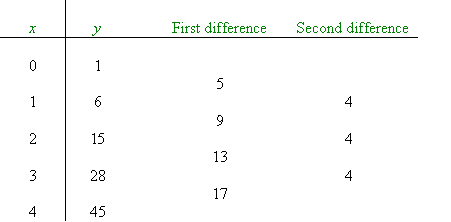
Finite differences

Finite differences

First Differences: The difference between consecutive y-values

Second differences: The differences between consecutive first differences and so on