Clasificación de los términos y elementos geométricos

Son ideas matemáticas abstractas, son términos no definidos, no existen en la realidad, pero se pueden concebir aisladamente por medio de consideraciones abstractas o primitivas.

Es la marca que deja la punta fina de un lápiz y que carece de dimensiones; se define también como la intersección de dos rectas se lo determina por una letra mayúscula.

Es el conjunto infinito de puntos que siguen una misma dirección, que tienen una sola dimensión: la longitud, también se define como la intersección de dos planos. Una recta se nombra mediante una letra minúscula o mediante dos letras mayúsculas situadas en dos puntos cualesquiera de ella.

Es una parte de la recta que tiene un punto inicial o también porción de una recta comprendida entre un punto llamado origen y el infinito.

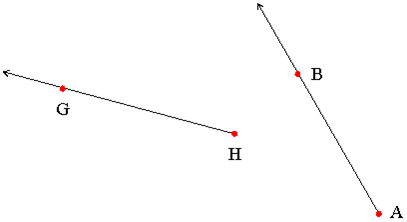
Son aquellos que pertenecen a una misma recta, pero tienen sentido contrario.

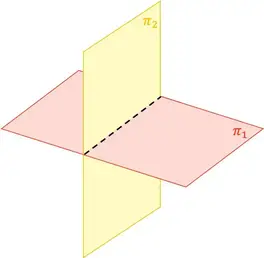
Es el conjunto infinito de puntos que tiene dos dimensiones: largo y ancho, se determina con una letra mayúscula o con letras del alfabeto griego. El plano no tiene límite y solamente podemos representar una parte de él, se lo puede representar por una hoja de papel, la superficie de una mesa, de una pared.

Es el conjunto infinito de puntos que tiene tres dimensiones: largo, ancho (espesor), y altura; se lo representa mediante los sólidos o volúmenes geométricos.

Un sólido es un espacio limitado cualquiera con tres dimensiones.

Dos números reales o bien son iguales o bien son diferentes.

Un número real es igual a sí mismo.

Si un número real es igual a un segundo, entonces el segundo es igual al primero.

Si un número real es igual a un segundo, y este segundo es igual a un tercero entonces el primero es igual al tercero.

Si a los dos miembros de una igualdad se adiciona un mismo número real, la igualdad no altera.

Si a los dos miembros de una igualdad le multiplicamos un mismo número real, entonces la igualdad, no cambia.

Si a cada miembro de una igualdad le suprimimos un mismo sumando o un mismo factor entonces la igualdad no altera.

La suma o multiplicación de dos números reales es otro real único.

Los términos o factores reales pueden asociarse de cualquier manera, el resultado no varía.

El cero es el elemento idéntico o módulo en la adición.El uno es el elemento idéntico o módulo de la multiplicación.

Para todo número real existe un número −𝑎 (opuesto).

La variación del orden de los sumandos o de los factores no altera la igualdad.

Distributivo con respecto a la suma.

Para todo número real, se satisface una de las siguientes condiciones: ∀a, ∀b:𝑎 ≠ 𝑏 → 𝑎 > 𝑐 ∨ 𝑎 < 𝑐

Si un número real es menor que un segundo, entonces el segundo no es menor que el primero.

Si un número es mayor que un segundo y este mayor que un tercero entonces el primero es mayor que el tercero.

Si a los dos miembros de una desigualdad se les suma un número real entonces la desigualdad no altera.

Si a los dos miembros de una desigualdad los multiplicamos por un mismo número real positivo,entonces el sentido de la desigualdad no cambia.

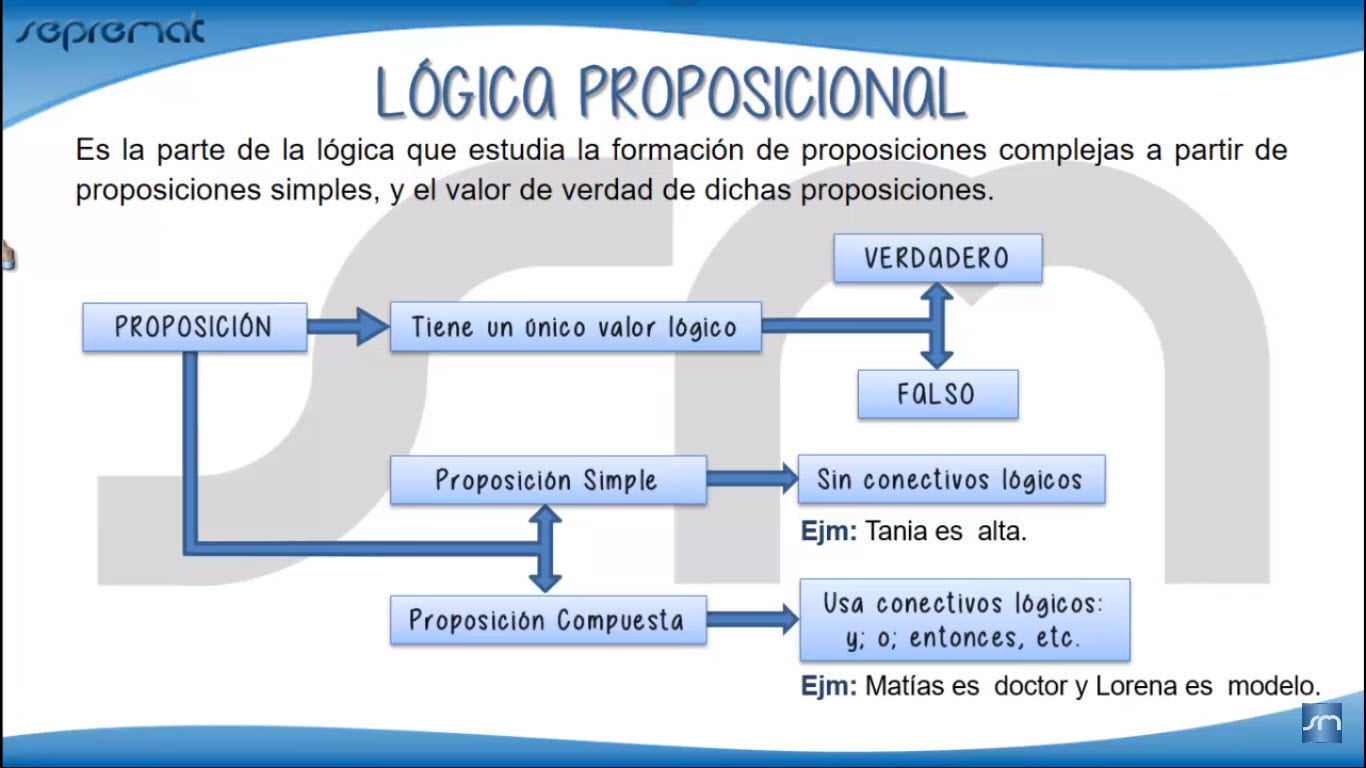
Es un enunciado cuyo valor de verdad es falso o verdadero, pero no verdadero y falso a la vez. Las proposiciones se las representa con: p, q, r, s, t...

Llámese axioma a una proposición que siendo evidente no requiere demostración. Es el resultado de la observación o experimentación: los axiomas son propiedades que se puede utilizar en cualquier asignatura.Ejemplo:Sí dos objetos son congruentes a un tercero, entonces son congruentes entre sí.

Es una proposición que, aunque no tiene la evidencia del axioma se admite sin demostración. A diferencia de los axiomas, estas son propiedades geométricas.

Es una proposición que es necesario demostrar utilizando definiciones, axiomas o postulados.En el enunciado de todo teorema se distinguen tres partes. La hipótesis, que es lo que se supone, la tesis que es lo que se quiere demostrar y la demostración que es el proceso lógico mediante el cual se demuestra la tesis.Ejemplo:La suma de las medidas de los ángulos interiores de un triángulo es igual a dos ángulos rectos.

Es una proposición que es consecuencia directa de un teorema, cuya demostración requiere poco o ninguno razonamiento nuevo.Ejemplo:La suma de los ángulos agudos de un triángulo rectángulo vale un recto.

Son proposiciones que parte de ciertos datos hasta llegar a ciertos resultados, los datos pueden ser gráficos o numéricos y los resultados de igual manera pueden ser gráficos y numéricos.