congruencia de triangulos
Carlos Enrique Garcia Milla Aguilar
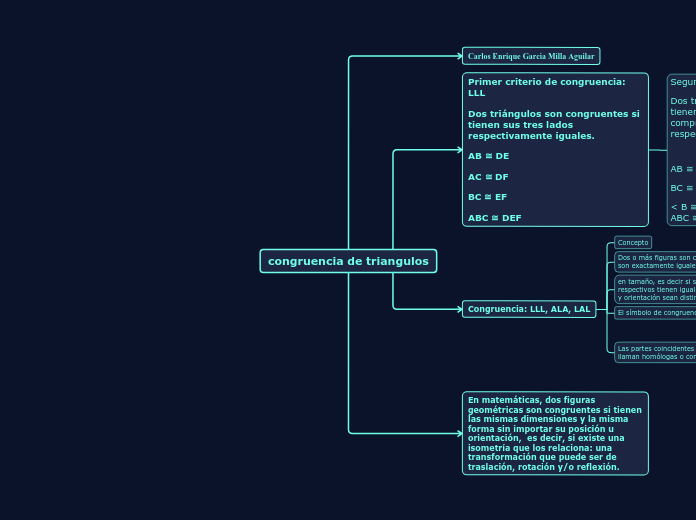
Primer criterio de congruencia: LLL
Dos triángulos son congruentes si tienen sus tres lados respectivamente iguales.
AB ≅ DE
AC ≅ DF
BC ≅ EF
ABC ≅ DEF
Segundo criterio de congruncia: LAL
Dos triángulos son congruentes si tienen dos lados y el ángulo comprendido entre ellos respectivamente iguales.
AB ≅ DE
BC ≅ EF
< B ≅ < E
ABC ≅ DEF
Tercer criterio de congruencia: ALA
Dos triángulos son congruentes si tienen respectivamente iguales un lado y los dos ángulos adyacentes a ese lado.
< B ≅ < E
< C ≅ < F
BC ≅ EF
ABC ≅ DEF
Congruencia: LLL, ALA, LAL
Concepto
Dos o más figuras son congruentes si se cumple que son exactamente iguales tanto en forma como
en tamaño, es decir si sus lados y sus ángulos respectivos tienen igual medida, aunque su posición y orientación sean distintas.
El símbolo de congruencia es ( ≅ ).
Las partes coincidentes de las figuras congruentes se llaman homólogas o correspondientes.
Criterios de congruencia
Los criterios de congruencia nos muestran la mínima información necesaria para afirmar que dos
triángulos son congruentes. Nos permiten identificar, con la información disponible, si dos triángulos
son o no congruentes entre sí.