conicas
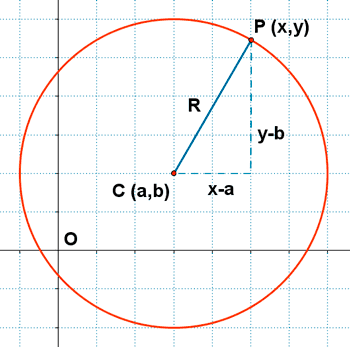
circunferencia
DEFINICION
Es el lugar geométrico de los puntos del plano que equidistante un punto fijo llamado centro. La distancia del centro a un punto cualquiera de la circunferencia se llama radio.
ECUACION
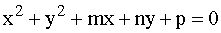
PARTES
1.CENTRO
Se trata de un punto ubicado en el interior y centro de una circunferencia. Este se encuentra a una misma distancia de los puntos del borde de la circunferencia.
2.RADIO
Es un segmento de la circunferencia que une el centro (punto central) con cualquier punto del borde. La longitud de este segmento es la mitad del diámetro, al igual que en las esferas, hiperesféras y círculos.
3.DIAMETRO
Se trata de un segmento que une dos puntos opuestos de una circunferencia, pasando por el centro. En otras palabras, es el segmento que al pasar por el centro, une los puntos externos de la circunferencia. La longitud del diámetro es igual a dos longitudes del radio.
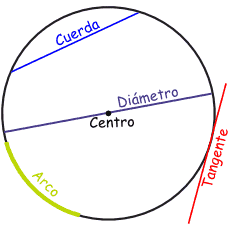
4.CUERDA
Se trata de un segmento que une dos puntos de una circunferencia. La cuerda de mayor longitud se conoce como diámetro.
5.ARCO
Se trata de cada parte dividida de una cuerda de la circunferencia. Este se denota con un símbolo sobre las letras que representan los puntos extremos del mismo arco.
6.RECTA SECANTE
Es aquella recta que corta a la circunferencia en dos puntos cualesquiera.
7.RECTA TANGENTE
Es aquella recta que corta a la circunferencia en un solo punto exacto, denominado punto de tangencia. Esta recta es perpendicular al radio.
8. PUNTO DE TANGENCIA
El punto de tangencia es aquel punto de contacto entre la recta tangente y la circunferencia.
9.SEMICIRCUNFERENCIA
El termino semicircunferencia representa al par de arcos delimitados por los extremos del diámetro de una circunferencia.
10.ANGULO CENTRAL
Es un ángulo que posee su vértice en el centro y sus lados son cuerdas correspondientes a radios.
11.ANGULO INSCRITO
Este es un ángulo donde sus lados pueden ser dos cuerdas cualesquiera, y cuyo vértice se encuentra en uno de los puntos de la circunferencia.
EJEMPLOS
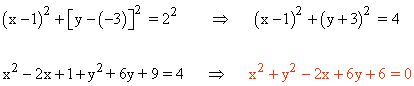
1) Hallar la ecuación general de la circunferencia que tiene de radio 2 y de centro (1, -3) .
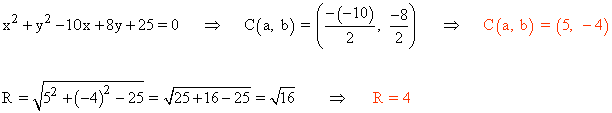
2) Calcular el centro y el radio de la circunferencia de ecuación x2 + y2 - 10x + 8y + 25 = 0

GEOGEBRA

elipse
DEFINICION
Dados dos puntos
F1 y F2 llamados focos, se denomina elipse al conjunto de puntos del plano tales que la suma de sus distancias a ambos focos es constante
ECUACION
E = { P ( x , y ) | d ( P , F 1 ) + d ( P , F 2 ) = c t e }

PARTES
1.FOCOS
Son los puntos fijos F y F'.
2 EJE FOCAL.
Es la recta que pasa por los focos.
3. EJE SECUNDARIO
Es la mediatriz del segmento FF'.
4. CENTRO
Es el punto de intersección de los ejes.
5. RADIOS VECTORES
Son los segmentos que van desde un punto de la elipse a los focos: PF y PF'.
6.DISTANCIA FOCAL
Es el segmento segmento de longitud 2c, c es el valor de la semidistancia focal.
7.VERTICES
Son los puntos de intersección de la elipse con los ejes: A, A', B y B'.
8.EJE MAYOR
Es el segmento segmento de longitud 2a, a es el valor del semieje mayor.
9.EJE MENOR
Es el segmento segmento de longitud 2b, b es el valor del semieje menor.
10.EJES DE SIMETRIA
Son las rectas que contienen al eje mayor o al eje menor.
11.CENTRO DE SIMETRÍA
Coincide con el centro de la elipse, que es el punto de intersección de los ejes de simetría.
EJEMPLOS

Subtema





Subtema

Subtema






Subtema

GEOGEBRA

parabola
DEFINICON
Dados un punto F (foco) y una recta r (directriz), se denomina parábola al conjunto de puntos del plano que equidistan del foco y de la directriz.
ECUACION
P{P(x,y)|d(P,r)=d(P,F)}

PARTES
1.VERTICE
Se trata del punto que intersecta la parábola con su eje, es decir, el punto que coincide con el eje focal o que cruza con este. Es también, el punto medio entre la directriz y el foco. En pocas palabras, es aquel punto que corta el eje focal de la parábola. Este se designa con la letra V.
2.FOCO
Se trata de un punto singular, es decir, que no pertenece a la parábola. Este se considera un punto fijo de referencia, el cual está ubicado sobre el eje focal. Es respecto al foco que cada punto de la parábola tiene una misma distancia hasta una recta llamada directriz. Este es designado con F.
3.DIRECTRIZ
Se trata de una línea o recta fija que determina las condiciones de generación de alguna otra línea. Esta se encuentra perpendicular al eje focal ubicado a una determinada distancia del vértice de la parábola. Esta se designa con la letra d.
4.EJE FOCAL O DE SIMETRÍA
Se trata de una línea recta, perpendicular a la directriz, que pasa por el foco. Esta se emplea para dividir simétricamente a la parábola.
5.PARÁMETRO O DE DISTANCIA FOCAL
Es aquella que indica la magnitud de la distancia entre el vértice y la directriz, igualmente de esta y el foco. Ambas distancias son iguales ya que están en la misma línea recta perpendicular a dicha directriz. En pocas palabras, corresponde a la distancia que hay entre la directriz y el foco de una parábola. El parámetro se designa con la letra p.
6.RADIO VECTOR
Es un segmento que conecta un punto cualquiera, perteneciente a la parábola, con el foco.
7.CUERDA
Corresponde a un segmento que conecta dos puntos de la parábola.
8.CUERDA FOCAL
Es la cuerda, o segmento, que pasa por el foco.
9.LADO RECTO
Este corresponde a un segmento que se encuentra perpendicular al eje de simetría. Este pasa por el foco y está paralelo a la directriz. Los extremos del lado recto son puntos de la parábola (A, B). Este suele designarse con las letras LR.
EJEMPLOS
Hallar la ecuación de la parábola de directriz x=4 y foco F(–2,0)
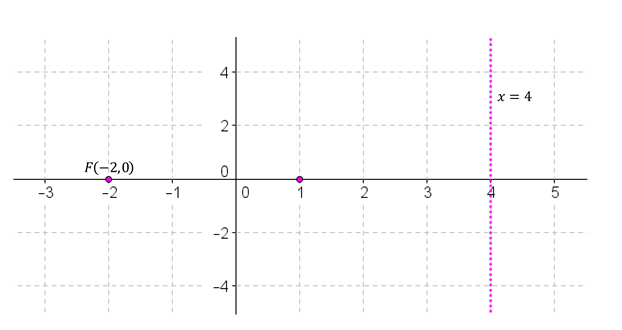
|c|=d(V,F)
V=(–2+42,0)=(1,0)
(y–β)2=4c(x–α)
(y–0)2=4c(x–1)
|c|=d(F,V)=3|c|=d(F,V)=3
y2=–12(x–1)
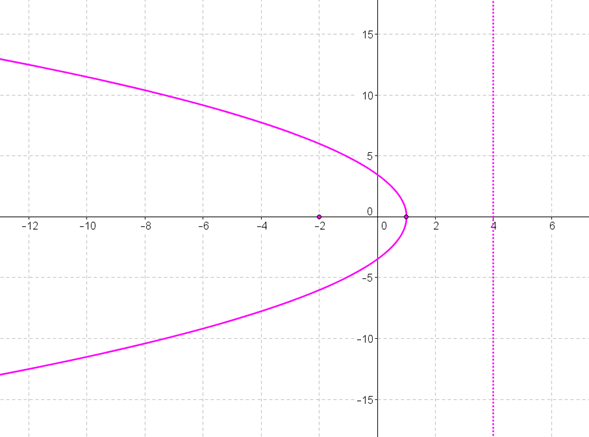

GEOGEBRA
Subtema

hiperbola
DEFINICION
Dados dos puntos F1 y F2 llamados focos, se denomina hipérbola al conjunto de puntos del plano tales que el valor absoluto de la diferencia de sus distancias a los focos es constante.
ECUACION
Subtema
H={P(x,y)||d(P;F1)d(P;F2)|=2a=cte}
Subtema
1. FOCOS
Son los puntos fijos F1 y F2 en los que la diferencia de distancias es constante a cualquier punto X en valor absoluto.
2.RADIO VECTOR
Se conoce como la distancia R de un punto (P) en algún foco.
3.EJE FOCAL O EJE TRANSVERSO
Eje de simetría E que conecta los dos focos.
3.EJE NO TRANSVERSO
Mediatriz T que posee el eje focal.
4.CENTRO
Punto medio O de ambos focos. Es la intersección entre el eje transverso y focal.
5.VERTICES
Puntos de intersección (V1 y V2) que tiene el eje focal junto con la hipérbola.
6.DISTANCIA FOCAL
Distancia que existe entre los focos (2c). También se puede representar como F1F2.
7.EJE REAL O MAYOR
Distancia que tienen los vértices. (2a)
8.EJE IMAGINARIO O MENOR
Se entiende como la distancia 2b que tienen los puntos B1 y B2. Estos puntos se crean en el proceso de relaciones entre semiejes, representándose con la siguiente fórmula: c2 = a2 + b2
9.ASINTOTAS
Las asíntotas son dos líneas en forma recta (A1 y A2) que tiene una aproximación en el infinito sin llegar a interceptar en la hipérbola. Las asíntotas se ubicarán a una distancia 0 de la hipérbola cuando están en el infinito. Es posible obtener las ecuaciones de las asíntotas al conocerse el semieje real (a) y el semieje imaginario (b).
10.PUNTOS EXTERIORES Y ANTERIORES
Son los puntos que se encuentran dentro de las regiones con un foco, unos son interiores (I) y otros son exteriores (Ex). Esto se debe a que la hipérbola divide el plano en tres regiones, las cuales dos de ellas tienen un foco y la restante no tiene
11.TANGENTES DE LA HIPERBOLA
La tangente se conoce como la bisectriz que tienen los dos radios vectores de un punto Pi. Sobre cada uno de estos puntos Pi están las ramas de la hipérbola.
12.CIRCUNFERENCIA PRINCIPAL
Representa ser la ubicación geométrica donde se encuentran las proyecciones que tiene un foco sobre las tangentes. Su centro es 0 y su radio r=a.
13. DIRECTRICES DE LA HIPERBOLA
Rectas que son paralelas al eje transverso (D1 y D2). La distancia que existe entre cada una es a/e, atraviesan las intersecciones de la circunferencia principal usando las asíntotas. (A1 y A2)
14.HIPERBOLA EQUILATERA
Posee las asíntotas (A1 y A2) de manera perpendicular entre sí, esto sucede al formarse un ángulo con cada uno de los ejes de 45°.
15.EXCENTRICIDAD
La excentricidad de la hipérbola se encarga de medir la abertura de la misma. La semidistancia focal representada como c es siempre mayor que el semieje real (a). La excentricidad de la hipérbola siempre es mayor a la de la unidad.
EJEMPLOS
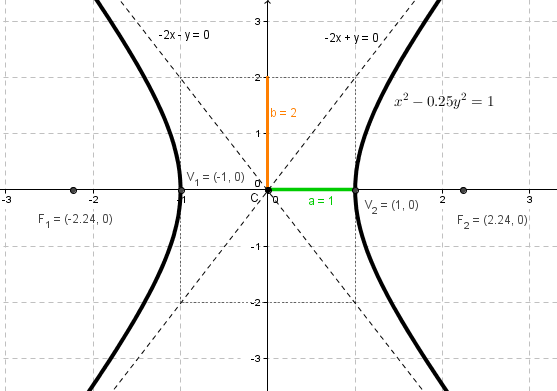
Hallar la gráfica de la curva definida por la ecuación:
x2–y24=1
C(0,0)
Semiejereal:a=1
Semiejeimaginario: b=2
Semidistanciafocal:c=√12+22=√5
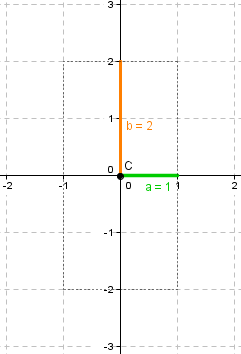
V1(1,0)
V2(–1,0)
F1(–√5,0)
F2(√5,0)
Asíntotas:y=±2x
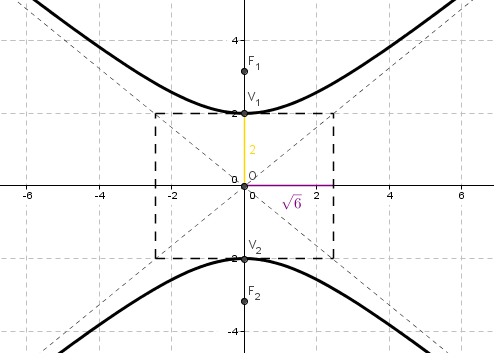
Hallar la gráfica de la curva definida por la ecuación:
Y2/4–X2/6=1
a2=4→a =2 semieje real
b2 =6→ b=√6 semieje imaginario
Vértices (0,±2)
c2=a2+b2⇒c2=10→c=√10
Focos (0,±√10)
Subtema
y=2√/6 x , ,y=–2/√6 x

GEOGEBRA
