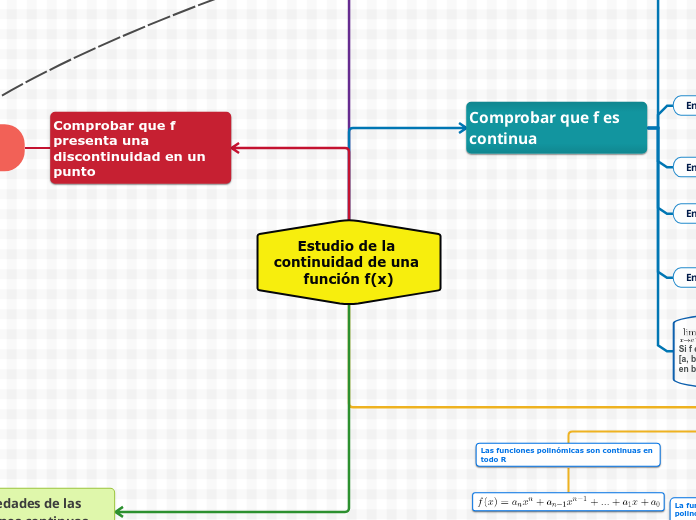
Estudio de la continuidad de una función f(x)
Idea intuitiva
Que no haya que levantar el lápiz del papel al dibujar la gráfica de una función cuando pasemos por los puntos en los que está definida.
Comprobar que f es continua
En un punto x=a
Cumplir las siguientes condiciones
Que exista el límite de f(x) en el punto x=a
Que exista f(a)
Que el límite de f(x) en x=a coincida con f(a)
Si no las cumple
f(x) es discontinua en el punto x=a
f es continua por la derecha en a, si
f es continua por la izquierda en a, si
En un intervalo cerrado [a,b]
Si cumple
Continua en todos los puntos pertenecientes a dicho intervalo
En un intervalo abierto (a,b)
Cuando f es continua en cada uno de sus puntos
En un intervalo (a,b]
Si cumple
Continua en todos los puntos pertenecientes a dicho intervalo
En un intervalo [a,b)
Si cumple
Continua en todos los puntos pertenecientes a dicho intervalo
Si f está definida solamente en el intervalo [a, b] y se dice que f(x) es continua en a o en b, se entiende en el sentido de que
Funciones elementales
Las funciones polinómicas son continuas en todo R
La función racional con P(x) y Q(x) polinomios es
continua en todo R excepto los x que anulan el denominador.
Funciones racionales
La función irracional es continua en
Todo R si n es impar
En todos los x talque P(x) es mayor
o igual que cero si n es par
Función irracional
La función exponencial es continua en todo R
Función exponencial
La función logarítmica es continua en todos los números reales estrictamente
Es continua en todo su dominio
Si fuera
f(x) sería continua en los valores de x para los que
Son continuas en todo R
Es continua en todo R excepto en
Comprobar que f presenta una discontinuidad en un punto
Dependiendo de cuál de las tres condiciones que determinan la continuidad de una función en un punto x=a falle
PERO FINITO
Discontinuidad evitable
Decimos que f tiene una
discontinuidad evitable
en el punto x=a
Si queremos que f sea continua en x=a, se `puede definir una nueva f con
Inevitables o esenciales
O los dos son infinitos
De salto infinito
Decimos que f tiene una discontinuidad inevitable de salto infinito en x=a.
Ambos existen y finitos
De salto finito
Decimos que f tiene una discontinuidad inevitable de salto finito en x=a.
Cuando el límite de f en un punto no existe, aún cuando la función no tiende a infinito.
Ejemplo
Propiedades de las funciones continuas
Si f y g son funciones continuas en x=a
Son continuas en x=a
f(x)+g(x)
f(x)-g(x)
f(x) · g(x)
Función compuesta
Si f es continua en x=a y g es continua en f(a)
Es continua en x=a