Fundamentals of Elementary Math

We talked about a problem about a case of coke, the case of coke may be looked at as a whole in many different ways, this was the case in this problem.
It could be stated that "I took 18 home", in which case the viewer considered each individual can a whole.
It could be stated as "I took 1 and 1/2 home, refferring to the rows of coke as each whole. There are many different ways of viewing a whole, and none of them are incorrect.

We then did a problem on how to find a whole, when you know a fraction of it. For example, is 6 stars is 3/5, then how many stars are in 1 unit? (5/5) In this problem, 10 stars is a whole.

Unit Iteration
Consistently repreating a unit to build a whole

Partitioning
Splitting the whole into equivalent parts

Fractions are out of one WHOLE thing, not multiple!

Do NOT say 1 out of 5

DO say 1, one fifths

Numerator: the NUMBER of pieces
Denominator: the DENOMINATION (size) of pieces

We worked with wooden shapes to practice and further learn about wholes and fractions.

Mixed Numbers

47/36

You can find the mixed number by
36/36+ 11/36= 47/36

36/36= 1 Whole
11/36

1 and 11/36 is your mixed number.

How many wholes can you make?!

This week we started with different ways of representing things, I.E.; Write/Draw everything you can that represents 3/4.

Many of us drew circles and rectangles, the rectangle proved to be the best choice.

Spatial Relationships: have a picture of the number, including where it lies on the number line

Benchmarks: 0, 1/2, 1, 1&1/2. Is it above or below 1/2? How far away is it from 1?

Part-part-whole: Knowing 3/4 can be broken into parts; 1/2+1/4, 1/4+1/4+1/4+1/4

We went into further detail of this and related it to decomposing.

How can 7/8 be decomposed?

7/8+0
6/8+1/8
5/8+2/8
4/8+3/8

7/8+3/8

7/8+ (1/8+2/8)

8/8 + 2/8
1 whole and 2/8

Tell which fraction is greater
3/7 < 5/8
1/24 < 17/32
3/8 < 4/10
6/7 < 8/9

We found a lot of these answers through benchmarks

We solved the more complex ones through placing them on number lines

In expanded form, every single number is represented seperately

1342

1000+300+40+2

To further expand it you can..

(1X10)^3+(3X10)^2+(4X10)^1+(2X10)^0

EXPANDED FRACTIONS

12.47

10+2+.4+.07

12345.6789

One is always the balance point!

10^4 10^3 10^2 10^1 10^0 10^-1 10^-2 10^-3 10^-4
1 2 3 4 5 . 6 7 8 9

10000 1000 100 10 BALANCE 1 1 1 1
_____ ___ ___ __ __ ___ ____ _____
1 1 1 1 10 100 1000 10000

12.47

(1X10)^1+(2X10)^0+(4X10)^-1+(7X10)^-2

100% of 72 = 72
50% of 72= 36
25% of 72= 18
75% of 72= 54
10% of 72= 7.2
5% of 72= 3.6
15% of 72= 10.80
20% of 72= 14.40
40% of 72= 28.80

Finding simple percentages is easy, by just making something similar to a ratio table.

Using number lines

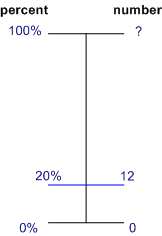
It is a visual way to solve percentage problems.

In this picture, the answer is 60.

Miah had 4/6 of a pan of browines left, and Sarah wants to buy 3/4 of what's left

______________________
l XXXXXXXXXXXXXXXXXXXl
l XXXXXXXXXXXXXXXXXXXl
l XXXXXXXXXXXXXXXXXXXl
l XXXXXXXXXXXXXXXXXXXl
l l
l_____________________l

X= 4/6 of what is left
X= 3/4, what Sarah bought

This technique proved to be very effective when multiplying fractions

The correct way to "cancel out"

5 3
_ X _

7 5

3X7
___

7X5

*Use associative property of multiplication to switch the numbers

3X7 3 7
___ --> __ X __ (1)

5X7 5 7

EQUALS
3
_

5

3/5 +7/10

3/5 +(4/10+3/10)

1 3/10

Decomposing the numbers, to make a whole
(You find numbers you can break out of the second one, to get closest to a whole)

7 1/3 - 4 3/4

<---4&3/4---5----------------7-----7&1/3--->
__ __________ ____
1/4 2 1/3

1/4+2+1/3

2+ 3/12 + 4/12

2 7/12

Finding the distance between two fractions can give you the answer without using dificult subtraction!

Partition

The dividend split into the divisors groups

Repeated subtraction

Subtracting the divisors from the dividend

Remember that when working with whole numbers, there is still an invisible denominator!

The traditional way we were taught is very simple, but can be very confusing for kids. And is also frustrating because many of us were not taught why it works.

We were taught to flip the second fraction, and multiply across.

2 3
_ / _

5 2

2 2
_ X _

5 3

4
_

15

Dividing with common denominators is very simple, because the denominators cancel out, and you are just left dividing the top numbers.

The proper way to write ratios is with a colon, or to write it out

2 boys, to 34 girls

2:34
or
2 to 34

One fruit basket is 15$
How many fruit baskets can you buy with 135$?

1 l 2 l 10 l 5 l 9
__________________
15 l 30 l 150l 75 l 135

PRACTICE

Molly bought six heads of cabbage for 9.30. If willie buys 22 heads at the same price per head, how much will it cost him?

6 l 3 l 12 l 2 l 10 l 22
____________________________
9.30 l 4.65l 18.60 l 3.10 l 15.50l 34.10