MPM2D0 Final Exam
Linear Systems
A Linear Systemis composed of two or more linear relations.
To solve a Linear System you must determine which values of x and y are common to all lines. This occurs at the point of intersection.
Elimination
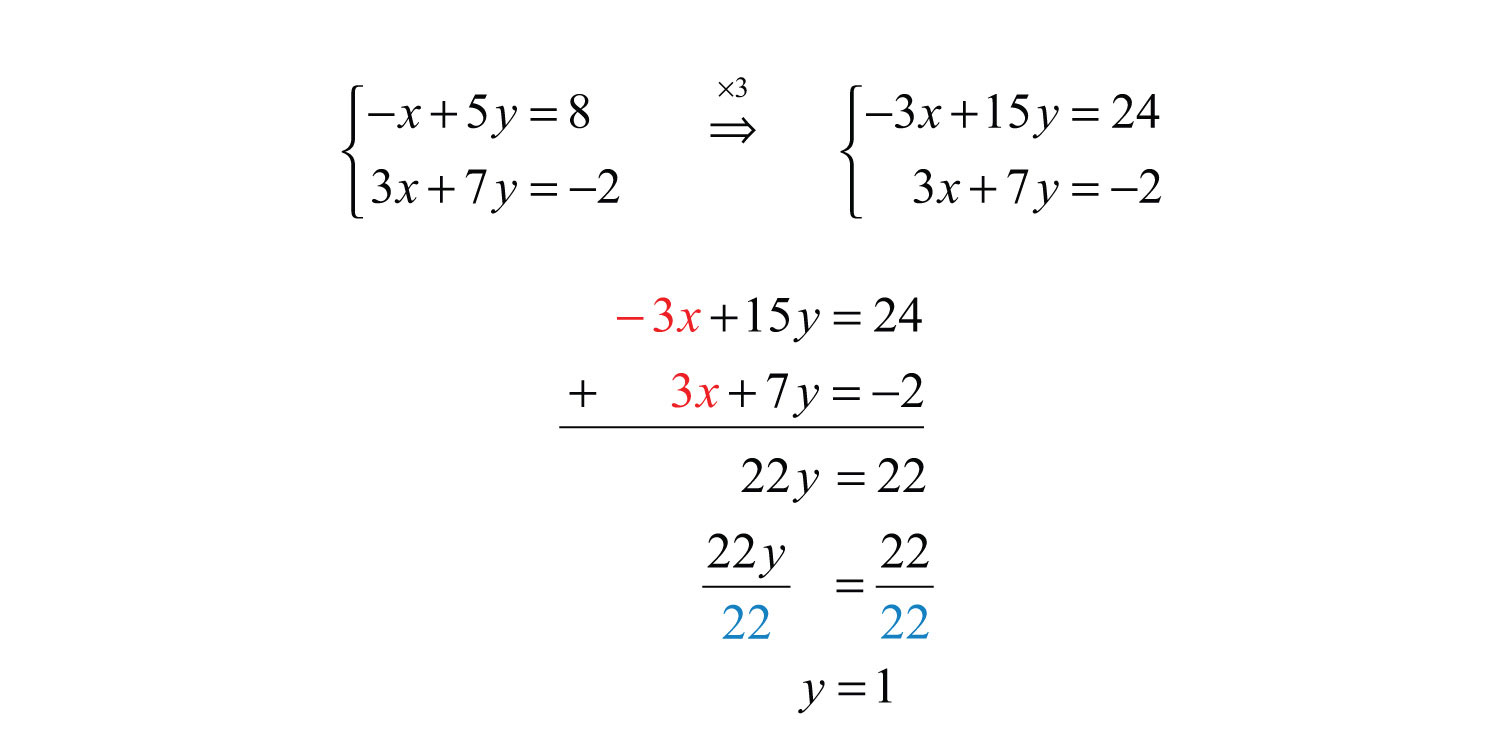
can only eliminate when the coefficient infront of both x's or both y's are equal and opposite signs
Substitution

Graphing

Only works when isolated for y for the y=mx+b format
m=rise/run
b=y intercept
Application
1)Assign variables to each of the unknowns
2)Write 2 equations showing the relationships between the variables. Each equation should include both variables.
3)Solve the system of equations using any method (graphing,substitution,elimination)
4)Check your solution
5)Clearly communicate your final answer
Quadratic Functions/Polynomials
Terms
Variable: A number used to represent an unknown quantity that can vary
Coefficient: A number in which the variable multiplies with eg. coefficient = 5: (5x)
Term: A set of numbers that multiply with each other (eg. 5x^2)
Degree of polynomial: the exponent after the variable in a polynomial (eg. x^2y^3. degree=5 (2+3)
Degree of Term: The highest exponent in a term
1st/2nd Differences
If 1st relations jump by the same, it is linear
If 2nd relations jump by the same, it is expontial
ax²+bx+c
"Golden Formula": Everything derives from this
Roots
if (x,y) = (a,0) & (b,0), then y=(x-a)(x-b)
TO GET THE ROOTS:
1.Get rid of any fractions by multiplying each term by the LCD.
2.Write equation as ax2+ x + c = 0
3.Fully factor.
4.Set each factor equal to 0 and solve using the zero product propert
Parabolas
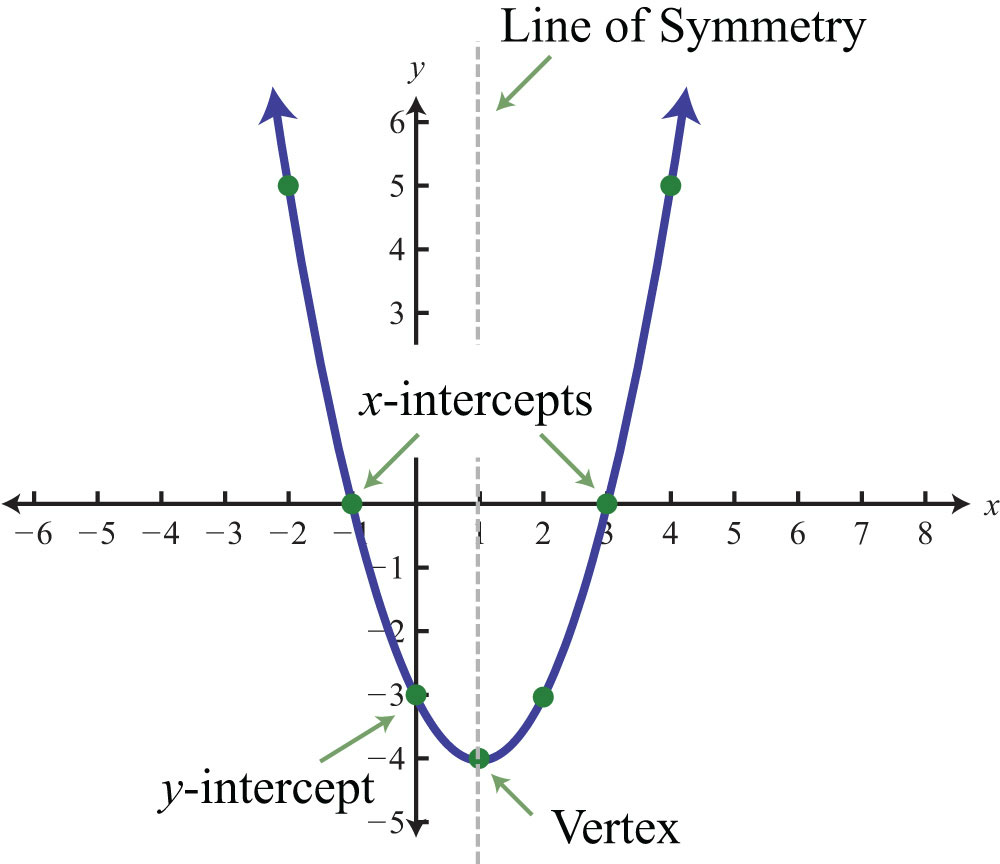
Properties of a Parabola
A parabola is a symmetrical graph, a 'U' shape. Its key components include:
Zeros: The points where the parabola intersects the x-axis (also called roots or x-intercepts).
Line of Symmetry: A vertical line that divides the parabola into two equal halves.
Minimum or Maximum: The lowest (minimum) or highest (maximum) point on the parabola.
Vertex: The point where the parabola meets the line of symmetry, which is also the minimum or maximum point.
Optimal Value: The y-coordinate of the vertex (either the minimum or maximum value).
Y-Intercept: The point where the parabola crosses the y-axis.

Forms of Quadratics, How to Factor
Standard Form: (ax²+bx+c)
Factoring Complex Trinomials
To get from Standard Form to Factored Form:
Find two numbers that add to "b" and multiply to "c"
1: ex. x²+5x+6
b=5, c=6
numbers that add to 5 and multiply to 6:
3 and 2
Therefore x²+5x+6=(x+3)(x+2)
To get from Standard Form to Vertex Form:
1: if a isn't 1, factor out a so that the other steps work (ex, 2x²+8x+3=2(x²+4x)+3
2: Complete the square by:
Take half of the coefficient of x, square it, and add it inside the parentheses. Subtract the same value to balance the equation
ex: x²+4x, half of 4 is 2, and 2²=4, so
2(x²+4x+4-4)+3
3: Simplify the Equation by removing the negative in the end of the bracket
2(x²+4x+4)+3-8
=2(x²+4x+4)-5
*dont forget to multiply the negative by a (2)
4: Write in vertex form (in the bracket is a perfect square trinomial.
2(x²+4x+4)-5
=2(x+2)²-5
Factored Form: (x-r)(x-s)
Derrives from standard form (ax²+bx+c)

Use distributive property to get to standard form
To get to Standard Form: Use Distributive Property, collect like-terms
To get to Vertex Form: Get to standard form and then (refer to "to get from Standard Form to Vertex Form)

Vertex Form: y=a(x-h)²+k
Vertex (h,k)
h=-b/2a, which is the Axis Of Symmetry
k=f(h)=y
Vertex (h,k)=(-b/2a, substitute h for k)
a = +, opens up. a = -, opens down
Special Cases (Completing the Square)

The expanded expression is called a DIFFERENCE OF SQUARES. Both terms are perfect squares and the terms are separated by a minus sign
To factor a difference of squares:
1)Two brackets that are the same but one with a plus (+) and one with a minus (-)
2)Square roots of perfect squares go in the brackets
In a perfect square trinomial, the first and last terms are perfect squares.
The middle term is twice the product of the square roots of the first and last terms
Quadratic Formula
Shows us the Roots of the Function
x=(-b±√(b²-4ac))/(2a)
THE DISCRIMINANT:
if √(b²-4ac)=0, 1 real solution
if √(b²-4ac)>0, 2 real solutions
if √(b²-4ac)<0, no real solutions
e
Distributive Property (Binomial Multiplication)
(a+b)(c+d)=ac+ad+bc+bd
Transforming Quadratics
Translations
Vertical Translations:
y=x^2 + k: moves the vertex up (k>0)
y=x^2 - k: moves the vertex down (k<0)
Horizontal Translations:
y=(x+h)^2: moves the vertex left (h>0)
y=(x-h)^2: moves the vertex right (h<0)
Reflections and Stretches
Reflections:
if a in ax^2 is negative, the parabola opens up and reflects over x-axis (vice versa)
Vertical Stretch/Compression:
if a>0, the parabola is stretched
if 0<a<1 (a is in between 0 and 1), the parabola is vertically compressed
Step Pattern
"Step pattern" refering to the jump in y value for each one x value
A parabola with a scale factor of 1 has a "step pattern" of 1, 3, 5
If a=2, the jumps are 2, 6, 10
Trigonometry
Sine Law
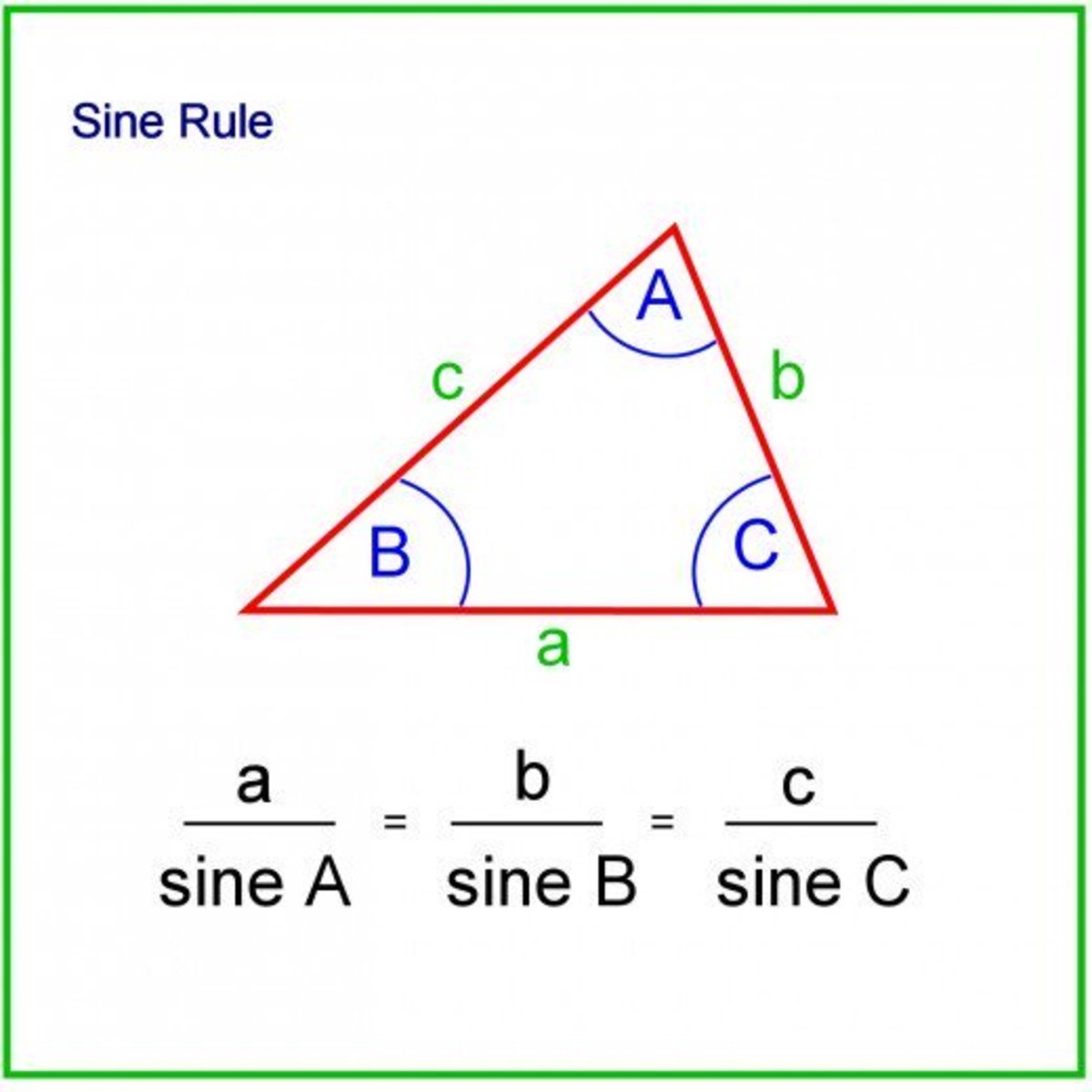
Use when you have:
AAS
SSA
ASA

EXAMPLE: solving for side b:
a/sin35=42/sin45
a = 42sin35/sin45
a = 34.07
*same method with side c
*SATT for angle C
Cosine Law
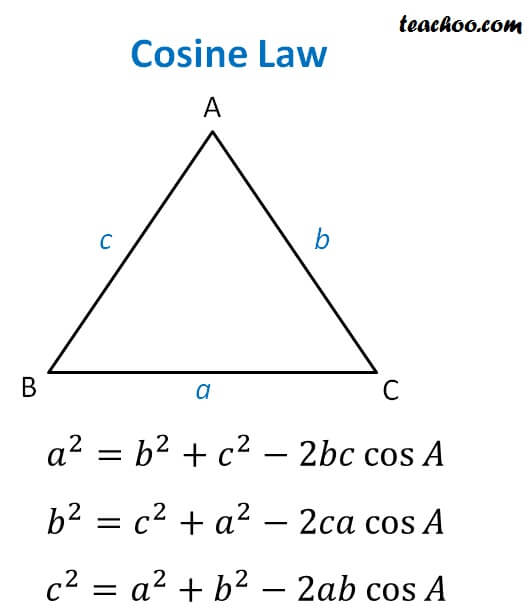
When solving for cosine(x), use algebra
Use when you have:
SSS
SAS
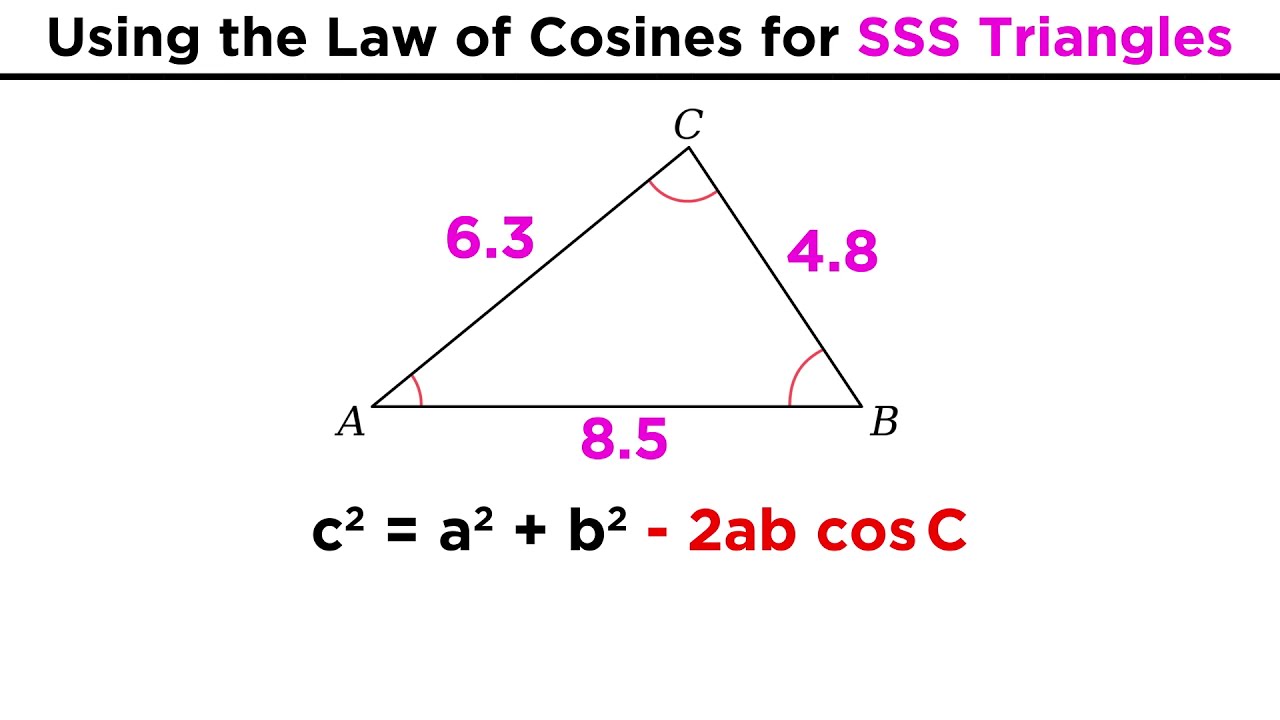
EXAMPLE: Solving for angle A:
4.8² =8.5²+6.3² -2(8.5)(6.3)(cosA)
cosA=(-8.5²-6.3²+4.8²)/(-2(8.5)(6.3))
cosA=127/153
A =33.9 degrees
*same method for other angles
SOH-CAH-TOA
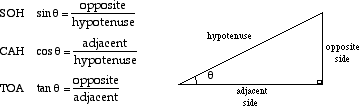
Inverse Signs:
θ=sin-1(o/h)
θ=cos-1(a/h)
θ=tan-1(o/a)
Similarity/Congruence

If the triangles have same angles but different side lengths, they are similar:
AB/AC=EG/EF, AC/BC=EF/GF, AB/BC=EG/GF
∠A=∠E, ∠B=∠G, ∠C=∠F
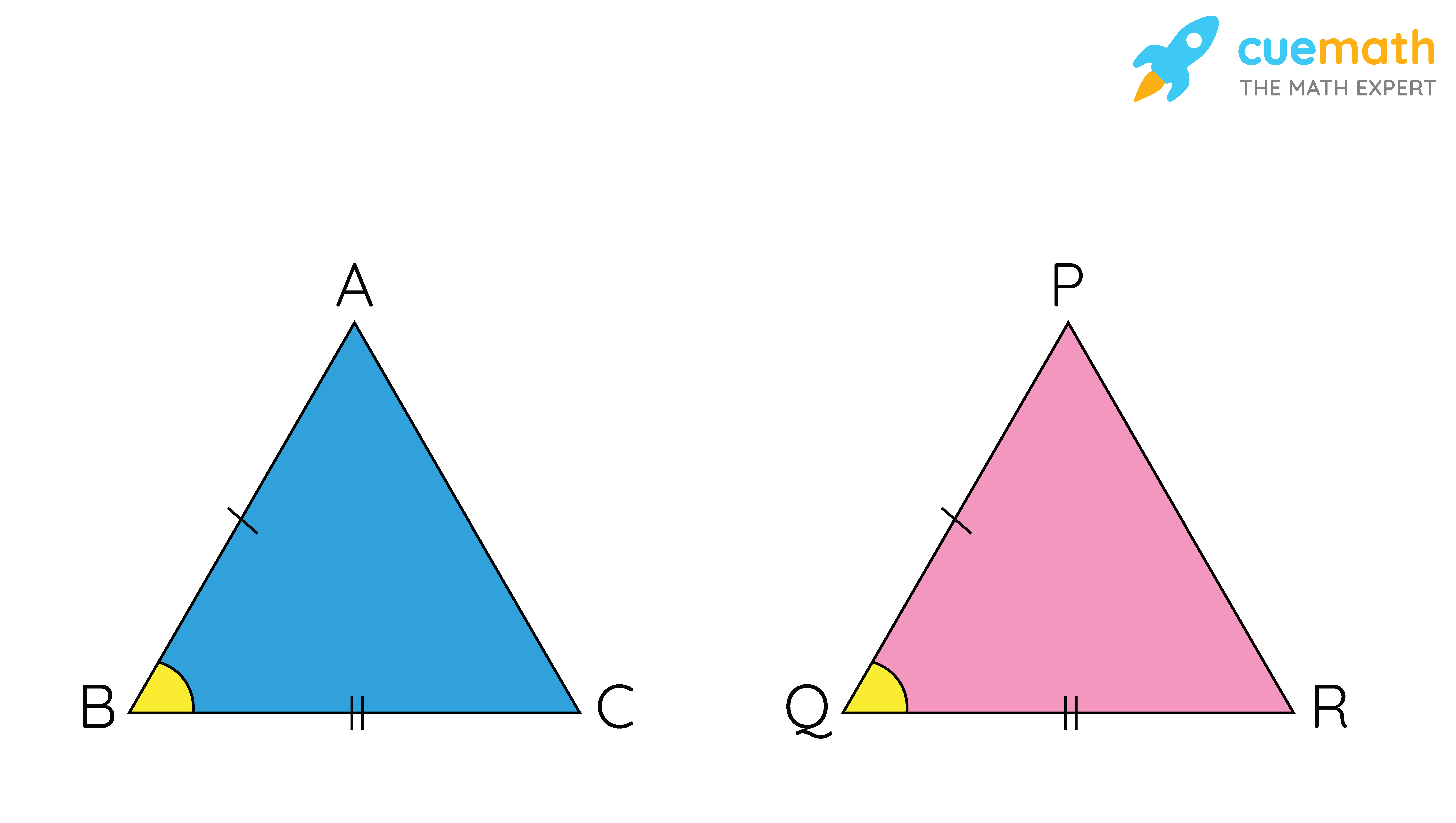
If the traingles have same side lengths and angles, they are congruent:
AB=PQ, AC=PR, BC=QR
∠A=∠P, ∠B=∠Q, ∠C=∠R
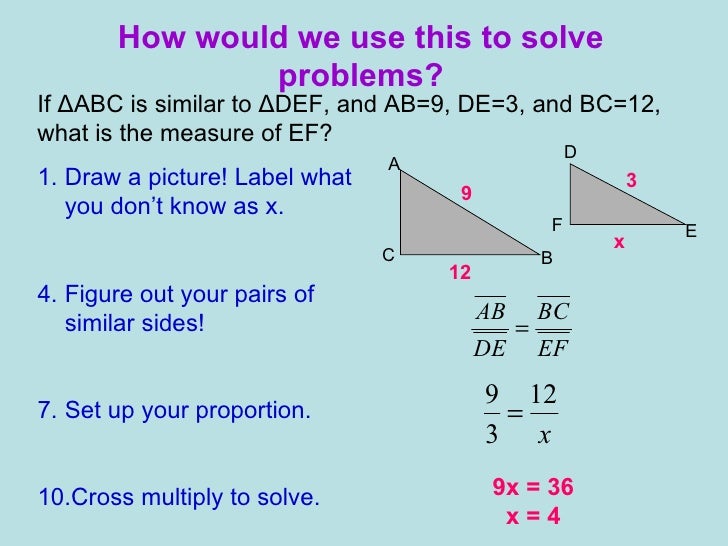
Solving Similar Triangles
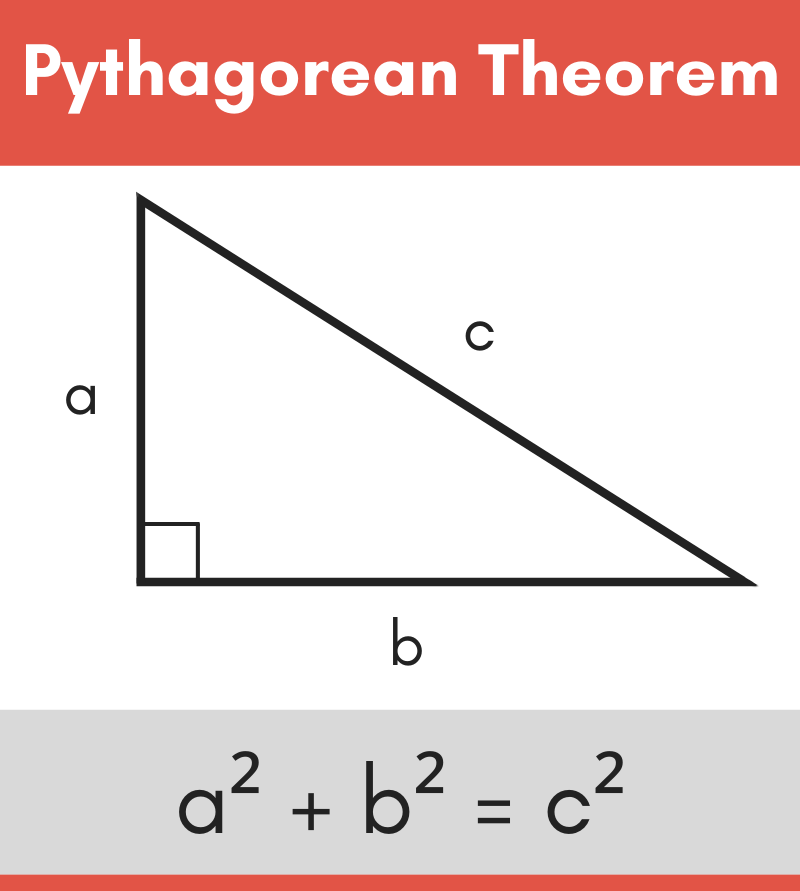
Also:
b^2=c^2-a^2
a^2=c^2-b^2
Analytic Geometry
Terms
Line Segment: A part of a line between two points
Midpoint: The point in the middle of a line segment
The line segment from a point in a triangle to the opposite side
Perpendicular: Two lines that form a 90 degree angle
Parallel: Two lines that never touch
Altitude: a line segment in a triangle from one vertex to the opposite side, creating a perpendicular line
Formulas

Slope of a line
EXAMPLE: Points (3,5) & (-2,6)
slope=(6-5)/(-2-5)
slope=-1/7
Equation of a line: y=mx+b
Midpoint of a line segment
EXAMPLE; Points (3,5) & (-7,-7)
midpoint=(-7+3)/2, (-7+5)/2
midpoint=(-2, -1)
√((x₂ – x₁)² + (y₂ – y₁)²)
Length of a Line Segment/Distance between Two Points
EXAMPLE: Points (4,1) & -3,-5)
x₂ – x₁=4-(-3)=7
y₂ – y₁=1-(-5)=6
Length of Line=√(7² +6²)
=√83
=9.11
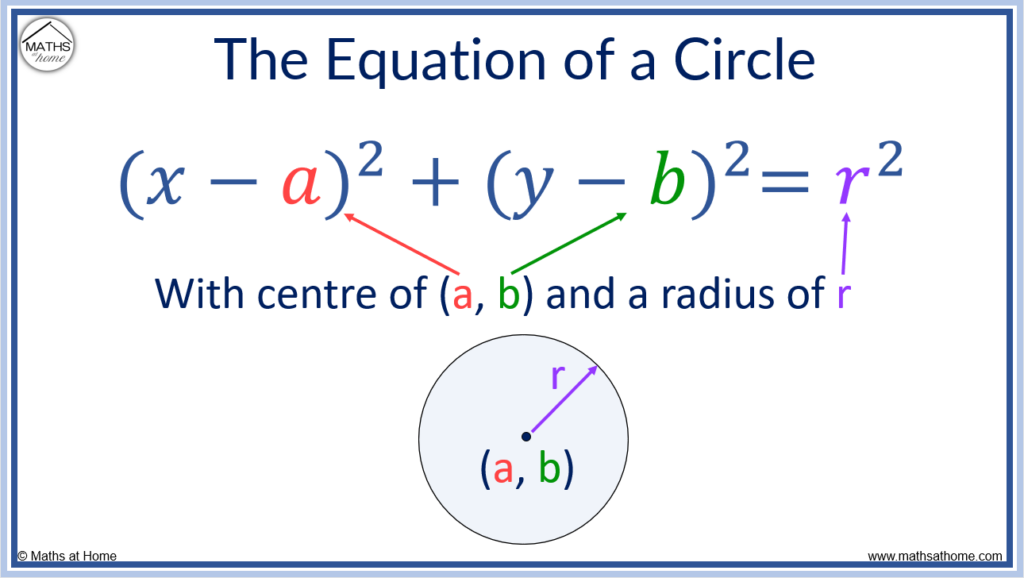
EXAMPLE: Centre at Origin, (x,y)=(2,2)
r^2=2^2+2^2
r^2=8
r=2.83
If Centre is at origin (0,0), then the equation is:
x^2+y^2=r^2
Tips
To Find The MEDIAN:
1)Find the midpoint of the opposite side
2)Find the slope of the line connecting the vertex to the midpoint of the opposite side
3)Calculatethe y-intercept of the line
4)Write the equation of the line.
To Find PERPENDICULAR LINE (RIGHT BISECTOR):
1: Flip the slope (eg. 2->1/2)
2: Change the sign (eg. 1/2->-1/2)
therefore: (2->-1/2)
To find the ALTITUDE:
1)Find the slope of the side opposite from the vertex
2)Find the slope of the altitude which is perpendicular to the side opposite from the vertex
3)Use the altitude’s slope and the point from the vertex to calculate the y-intercept of the altitude
4)Write the equation of the altitude

Classifying Figures
Exam Tips
Questions you don't understand, skip and come back to them
Dont rush, take your time
Think of questions fundamentally. If it doesn't make sense, it probably isn't right
Show work
Read questions carefully
Sleep well
Eat before
Don't forget Pencil, Eraser, Calculator, Ruler
Use "Therefore Statements" if it's a word problem
Line up equal signs
Dont stress out
Grade 9 Review
BEDMAS (Order of Operations: Brackets, Exponents, Division/Multiplication, Addition/Subtraction)
Y=MX+B (equation of a line
m=slope of line
b=y intercept
(x,y) can be anything on the x,y plane
Exponent Rules
a^b x a^c = a^(b+c)
a^b / a^c = a^(b-c)
Like Terms: Terms that can be grouped by adding or subtracting (x+y isn't xy.) (x + 3x=4x)