Sucesiones Reales
Definicion
Una sucesión de números reales es una aplicación del conjunto N (conjunto de los números naturales excluido el cero) en el conjunto R de los
números reales.
Se llama término de una sucesión a cada uno de los elementos que constituyen la sucesión. Para representar los diferentes términos de una sucesión se usa una misma letra con distintos subíndices, los cuales indican el lugar que ocupa ese término en la sucesión.
Tipos
CONVERGENCIA
MONOTONÍA
ALTERNADA Y OSCILANTE
ACOTADA
DISTANCIA AL LIMITE
El límite de una sucesión es el número al cual se van aproximando los términos de una sucesión.
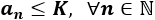
Una sucesión a(n) es acotada superiormente cuando ninguno de sus términos es mayor que algún número K
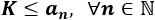
Una sucesión a(n) es acotada inferiormente cuando ninguno de sus términos es menor que algún número K
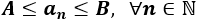
Una sucesión a(n) es acotada cuando es acotada superior e inferiormente
Una sucesión es alternada cuando cada término tiene el signo contrario que el del término que le precede.
Una sucesión es oscilante cuando:
-no es alternada y
-no es creciente ni decreciente ni constante.
Se dice que una sucesión de números reales es monótona creciente si cada término es menor o igual que el siguiente. Es decir los términos van aumentando su valor o, a lo sumo, son iguales. Por lo tanto, su representación en el plano cartesiano serán puntos que van subiendo.
Una sucesión a(n) es convergente cuando tiene límite finito. El límite L de una sucesión a(n) es el número al que la sucesión se aproxima cada vez más. Se dice que la sucesión a(n) converge a su límite L y se expresa por
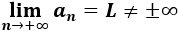
Ejemplos:

Subtopic
Secuencia Fibonacci
En matemáticas, la sucesión o serie de Fibonacci hace referencia a la secuencia ordenada de números descrita por Leonardo de Pisa, matemático italiano del siglo XIII:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…
A cada uno de los elementos de la serie se le conoce con el nombre de número de Fibonacci.
¿COMO SE CALCULAN LOS NUMEROS DE FIBONACCI?

1. Partiendo de los números 0 y 1, los números de Fibonacci quedan definidos por la función

2. Función generadora: Una función generadora para una sucesión cualquiera a0, a1, a2,… es la función f(X) = a0 + a1x + a2x2+…, es decir, una serie formal de potencias donde cada coeficiente es un elemento de la sucesión. Los números de Fibonacci tienen la función generadora:

3. Fórmula explícita: Esta manera de calcular los números de Fibonacci utiliza la expresión del número áureo: