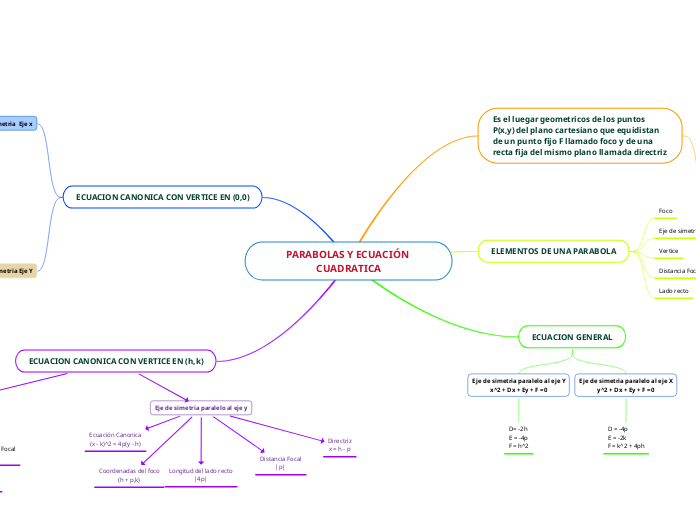
PARABOLAS Y ECUACIÓN CUADRATICA
Es el luegar geometricos de los puntos P(x,y) del plano cartesiano que equidistan de un punto fijo F llamado foco y de una recta fija del mismo plano llamada directriz

ELEMENTOS DE UNA PARABOLA
Foco
Eje de simetria
Vertice
Distancia Focal
Lado recto
ECUACION GENERAL
Eje de simetria paralelo al eje Y
x^2 + Dx + Ey + F =0
D= -2h
E = -4p
F = h^2
Eje de simetria paralelo al eje X
y^2 + Dx + Ey + F =0
D = -4p
E = -2k
F = k^2 + 4ph
ECUACION CANONICA CON VERTICE EN (0,0)
Eje de simetria Eje x
Longitud del lado recto
|4p|
Distancia focal
|p|
Directriz
x = -p
Coordenadas del foco
(p,0)
Ecuacion Canonica
y^2 = 4px
Eje de simetria Eje Y
Ecuacion canonica
x^2 = 4py
Coordenadas del foco
(0,p)
Directriz
y = -p
Distancia focal
|p|
Longitud del lado recto
|4p|
ECUACION CANONICA CON VERTICE EN (h,k)
Eje de simetria paralelo al eje X
Ecuación Canonica
(x - k)^2 = 4p(y - h)
Coordenadas del foco
(h + p,k)
Directriz
x = h - p
Distancia Focal
|p|
Longitud del lado recto
|4p|
Eje de simetria paralelo al eje y
Ecuación Canonica
(x - k)^2 = 4p(y - h)
Coordenadas del foco
(h + p,k)
Directriz
x = h - p
Distancia Focal
|p|
Longitud del lado recto
|4p|