Series Numéricas
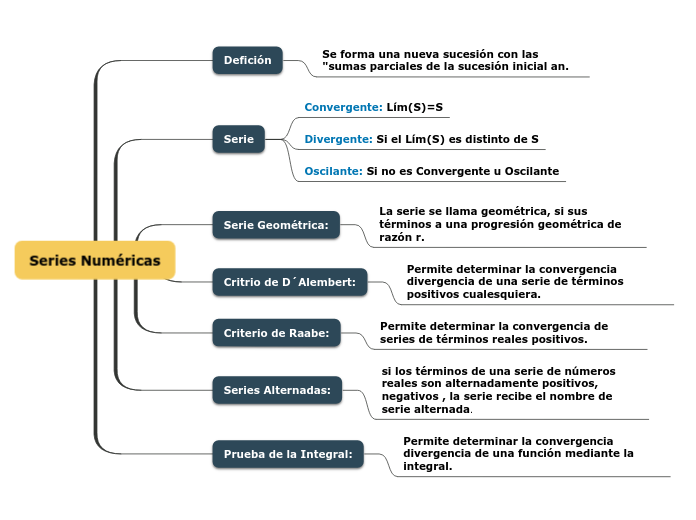
Defición
Se forma una nueva sucesión con las "sumas parciales de la sucesión inicial an.
Serie
Convergente: Lím(S)=S
Divergente: Si el Lím(S) es distinto de S
Oscilante: Si no es Convergente u Oscilante
Serie Geométrica:
La serie se llama geométrica, si sus términos a una progresión geométrica de razón r.
Critrio de D´Alembert:
Permite determinar la convergencia divergencia de una serie de términos positivos cualesquiera.
Criterio de Raabe:
Permite determinar la convergencia de series de términos reales positivos.
Series Alternadas:
si los términos de una serie de números reales son alternadamente positivos, negativos , la serie recibe el nombre de serie alternada.
Prueba de la Integral:
Permite determinar la convergencia divergencia de una función mediante la integral.