von Ledis Victoria Mercado Orozco Vor 2 Jahren
161
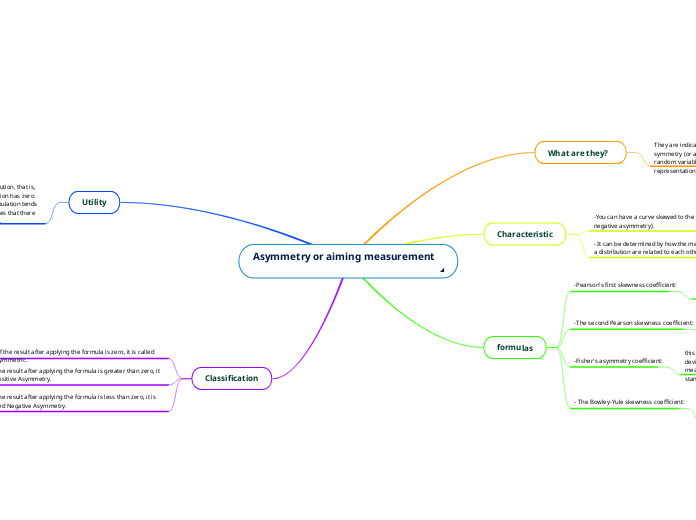
Asymmetry or aiming measurement
In statistical analysis, the concept of asymmetry or skewness is crucial in understanding the distribution of data. While many simplistic models assume a normal distribution that is symmetric about the mean, real-world data often exhibit skewness, where the distribution deviates from this symmetry.