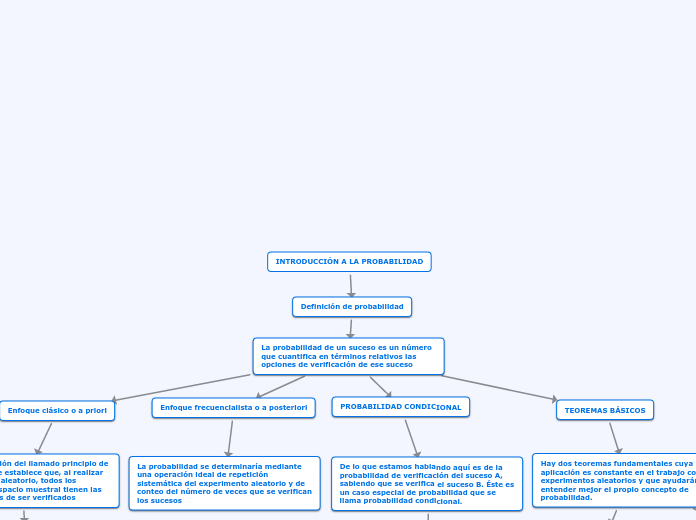
Enfoques de probabilidad
Enfoque matemático, axiomático o de Kolmogorov.
Este enfoque se presenta por medio de tres axiomas, los cuales son la fundamentación d toda la teoría de probabilidad.
Axioma 3
P(A U B) = P(A) + P(B)
Si A y B son eventos mutuamente excluyentes, entonces la probabilidad de su unión es la suma de sus probabilidades individuales.
La expresión anterior es generalizable a más de dos eventos, así:
P(A1 U A2 U A3 U … U An ) = P(A1) + P(A2) + P(A3) + … + P(An)
Axioma 2:
P(S) = 1 P( ø ) = 0
P(S)
representa la probabilidad de ocurrencia de algún resultado cuando se realiza un experimento aleatorio, y de acuerdo con el axioma 1, esta probabilidad debe ser 1. En consecuencia, la probabilidad del evento vacío debe ser 0.
Axioma 1
< = P(A) < = 1
Esto indica que la probabilidad de ocurrencia de un evento es un número, el cual debe oscilar siempre entre 0 y 1, sin contradecir la definición dada por Laplace en el enfoque clásico.
El extremo superior representa la certeza absoluta de la no ocurrencia del evento, mientras que el inferior representa la certeza absoluta de la no ocurrencia del evento. Cualquier otro valor entre 0 y 1 indica incertidumbre acerca de la ocurrencia del evento.
Enfoque empírico, frecuencia o a posteriori.
El enfoque empírico utiliza la frecuencia relativa como una aproximación al valor de la probabilidad de un evento, esto se refiere a un valor empírico de la probabilidad de ocurrencia del evento, la cual es un valor teórico resultante de un cálculo matemático.
Es conveniente por lo tanto tener, presente el concepto de frecuencia, como la cantidad de veces que ocurre un evento en un determinado periodo. Ahora bien, las frecuencias pueden ser absolutas o relativas:
Frecuencia relativa:
Es la fracción o porción de veces que se presenta un evento determinado en un experimento.
La frecuencia relativa para un evento A esta dada por:
fA: nA/n
P(A) = lim(n->inf)nA/n
Come se puede observar en la expresión anterior, la frecuencia relativa tiende a la probabilidad de ocurrencia del evento en el límite, es decir cuando el experimento se ejecuta un gran número de veces.
fA: (frecuencia absoluta)/(numero de ejecuciones del experimento)= (Numero de veces que ocurre A)/(Numero de ensayos)
Frecuencia absoluta:
Es el número de veces que se presenta un evento determinado en un experimento.
Enfoque clásico, a priori o de Laplace
Este enfoque define la probabilidad como un número, determinado de la siguiente forma: P(A)= (n(A))/(n(S))
Dónde:
N(A) = Cardinal del evento A.
La aplicación de este enfoque supone las siguientes condiciones:
Los puntos de S deben ser igualmente importantes, esto es, igual peso específico.
Trabaja con espacios muéstrales finitos.
S = Cardinal del espacio maestral S del experimento.