PARTIAL FRACTIONS

Mehr dazu

Unity3D_Hasten

von Mike Ton

Maintenance

von Wasana Wickramasinghe

Pessimism with a purpose

von aldemar yate

Elementary Mathematics

von cyndi silva

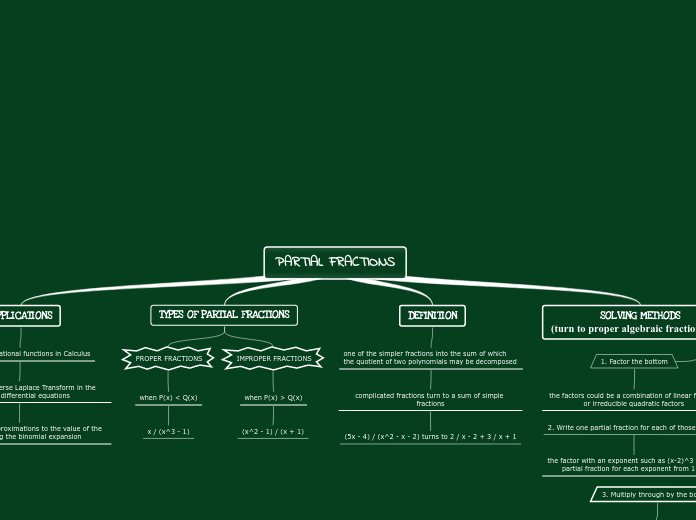
PARTIAL FRACTIONS

SOLVING METHODS (turn to proper algebraic fractions first)

4. Now find the constants A1 and A2

substituting zeros of the bottom

making a system of linear equations (of each power) and solving

3. Multiply through by the bottom

so no longer have fractions

2. Write one partial fraction for each of those factors

the factor with an exponent such as (x-2)^3 need a partial fraction for each exponent from 1 up

1. Factor the bottom

the factors could be a combination of linear factors or irreducible quadratic factors

DEFINITION

one of the simpler fractions into the sum of which the quotient of two polynomials may be decomposed

complicated fractions turn to a sum of simple fractions

(5x - 4) / (x^2 - x - 2) turns to 2 / x - 2 + 3 / x + 1

TYPES OF PARTIAL FRACTIONS

IMPROPER FRACTIONS

when P(x) > Q(x)

(x^2 - 1) / (x + 1)

PROPER FRACTIONS

when P(x) < Q(x)

x / (x^3 - 1)

APPLICATIONS

1. Integrating rational functions in Calculus

2. Finding the Inverse Laplace Transform in the theory of differential equations

3. Able to make approximations to the value of the function using the binomial expansion