Статистическая гипотеза-предположение о виде неизвестного распределения или об его параметрах.

Генеральная совокупность
Множество всех объектов, обладающих изучаемым признаком.
Объем генеральной совокупности-число объектов генеральной совокупности
Генеральная совокупность определяется задачей исследования.
Ho
Нулевая (или основная) – гипотеза о сходстве
Допустимая область – это область значений критерия, которые не противоречат нулевой гипотезе.
Мощность критерия – это способность выявлять различия или отклонять нулевую гипотезу, если она не верна.
если p - уровень больше 0,05, то нет оснований отвергать нулевую гипотезу

Альтернативная (или конкурирующая) – гипотеза о различиях
Направленная
Ненаправленная
Критическая область – это область значений критерия, при которых отвергается нулевая гипотеза и принимается конкурирующая.
если p - уровень меньше 0,05, то нулевую гипотезу отвергаем, принимаем конкурирующую (при уровне значимости 0,05)

Непараметрические критерии не базируются на предположении о виде распределения изучаемой величины и используют непосредственно выборочные данные, а не параметры выборки.
Нормальный закон распределения
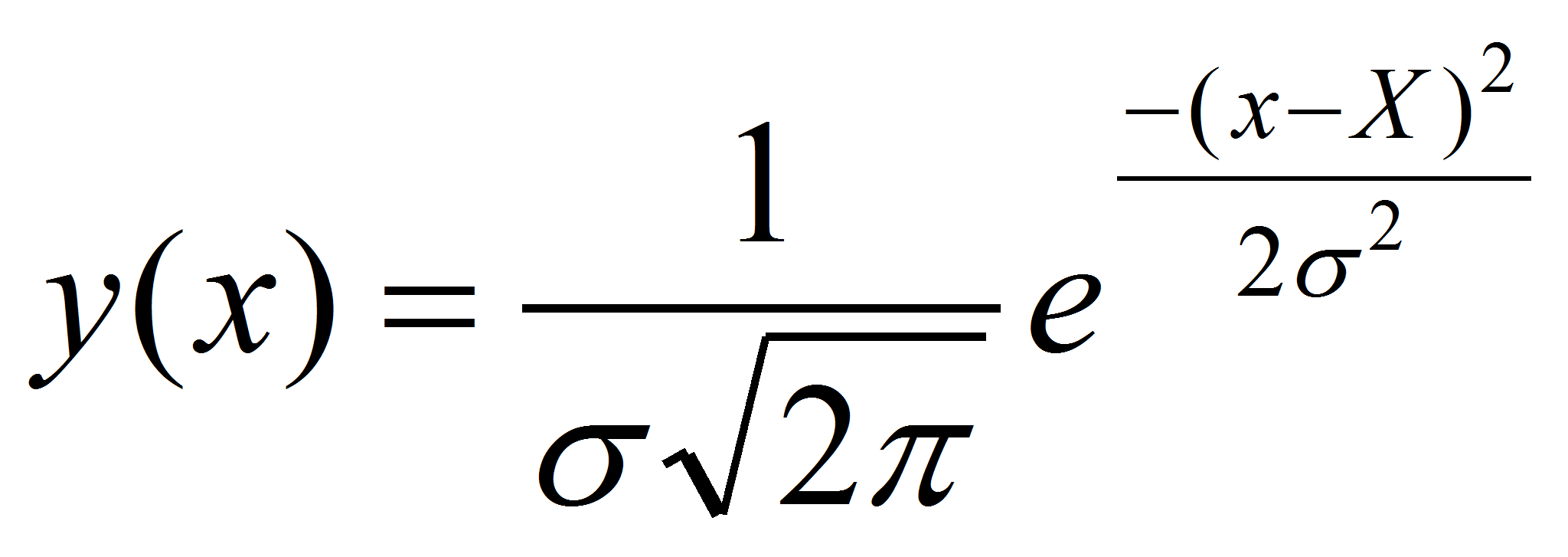

Правило трех сигм»: вероятность того, что значение нормально распределенной случайной величины отклонится от математического ожидания не более чем на 3σ, примерно равна единице.
Равенство средней арифметической,моды и медианы указывает на нормальность данного распределения
Чем больше величина признака отклоняется от среднего значения, тем меньше будет частота вероятности этого признака в распределении.
Выборочная совокупность
Множество объектов, отобранных случайным образом из генеральной совокупности для изучения
Количество объектов в выборке называют объемом выборки.
Репрезентативность - это показатель того, насколько хорошо выборка отражает основные свойства той генеральной совокупности, частью которой является.
Наблюдаемое значение критерия – это значение критерия, вычисленное по выборке, то есть зависящее от выборочных значений.
Зависимые выборки(связные)- если процедура эксперимента и результаты измерения, полученные на одной выборке, оказывают влияние на особенности протекания эксперимента и результаты измерения у другой выборки.

Если нулевая гипотеза отвергается и принимается конкурирующая, то выборочные средние различаются значимо, генеральные средние в исследуемых совокупностях не равны между собой.
Если нет оснований отвергать нулевую гипотезу, то выборочные средние различаются не значимо, генеральные средние в исследуемых совокупностях равны.
Независимые выборки(несвязные)- если процедура эксперимента и результаты измерения, полученные на одной из выборок, не оказывают влияния на особенности протекания эксперимента и результаты измерения у другой выборки.

Если гипотеза H0 отвергается и принимается гипотеза H1, то:
Генеральные средние не равны.
Выборочные средние различаются значимо.
Фактор влияет на исследуемую величину.
Если нет оснований отвергать гипотезу H0, то:
Генеральные средние равны.
Выборочные средние различаются незначимо.
Фактор не влияет на исследуемую величину.

Параметрические критерии основаны на конкретном виде распределения изучаемой случайной величины и используют числовые характеристики выборочной совокупности, которые являются точечными оценками параметров генеральной совокупности.
Гипотезы при использовании критерия Фишера-Снедекора выдвигаются следующим образом:
H0 - генеральные дисперсии равны
H1 - генеральные дисперсии не равны
Если в результате проверки нулевую гипотезу отвергаем, то генеральные дисперсии не равны, выборочные дисперсии различаются значимо.
Если нет оснований отвергать нулевую гипотезу, то генеральные дисперсии равны, выборочные дисперсии различаются не значимо.
Гипотезы при использовании критерия Стьдента выдвигаются следующим образом:
H0 - генеральные средние равны
H1 - генеральные средние не равны
Критерии согласия – это критерии, позволяющие оценить степень согласия наблюдаемого статистического распределения выборки с гипотетическим распределением.
H0 - функция распределения изучаемой величины соответствует функции нормального распределения
H1 - функция распределения изучаемой величины не соответствует функции нормального распределения
Наиболее часто для проверки согласия с нормальным законом применяются критерий Колмогорова-Смирнова и критерий Шапиро-Уилка