ALGEBRA BÁSICA
LOGARITMOS
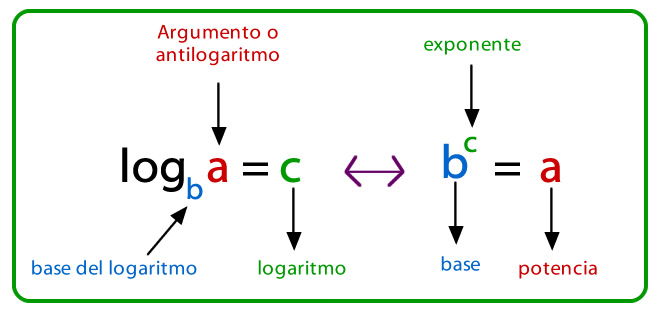
Un Logaritmo indica el exponente al que hay que elevar un número base para obtener el número original.
EJEMPLO (IMAGEN 9)
Propiedades generales de los logaritmos
1. En el campo de los números reales sólo existen logaritmos de números positivos. Los logaritmos de números negativos existen en el campo de los números complejos.
2. La base de un sistema de logaritmos es positiva y diferente de uno.
3. En todo sistema de logaritmos, el logaritmo de 1 es cero y el logaritmo de la base es 1.
TAMBIEN PUEDE SER
ANTILOGARITMO
Se define como la operación inversa a la logaritmación
COLOGARITMO
Se denomina cologaritmo de un número N > 0 , al logaritmo de su inverso multiplicativo en la
misma base.
Sistema de logaritmos
De la definición de logaritmo se deduce que cualquier número positivo, diferente de la unidad,
puede utilizarse como base de un sistema de logaritmos; por lo tanto, el número de sistemas de logaritmos es ilimitado.
LOS MAS UTILIZADOS SON
Sistema de logaritmos vulgares, decimales o de Briggs
Sistema de logaritmos naturales, neperianos o hiperbólico
RACIONALIZACIÓN
SE PUEDE RACIONALIZAR CUANDO
El denominador es un monomio
el factor racionalizante estará expresado por otro radical que tenga el mismo índice, pero cuyos exponentes del radicando estarán expresados por la diferencia existente entre el índice original de la raíz y los exponentes que afectan a las letras o número.
El denominador presenta radicales de la forma
el factor racionalizante estará expresado por la conjugada del denominador que se empleará tantas veces hasta que el denominador quede transformado en una expresión algebraica racional.
Factor racionalizante (F)
expresión irracional tal que al multiplicar a otra también irracional la convierte en una expresión racional.
ES
El proceso que consiste en transformar un denominador ( o numerador) irracional en otro
racional a través de un factor denominado factor racionalizante.
TEORÍA DE EXPONENTES
Tiene
por objeto estudiar todas las clases de exponentes que existen y las relaciones que se
dan entre ellos.
Operaciones que permite
Potenciación
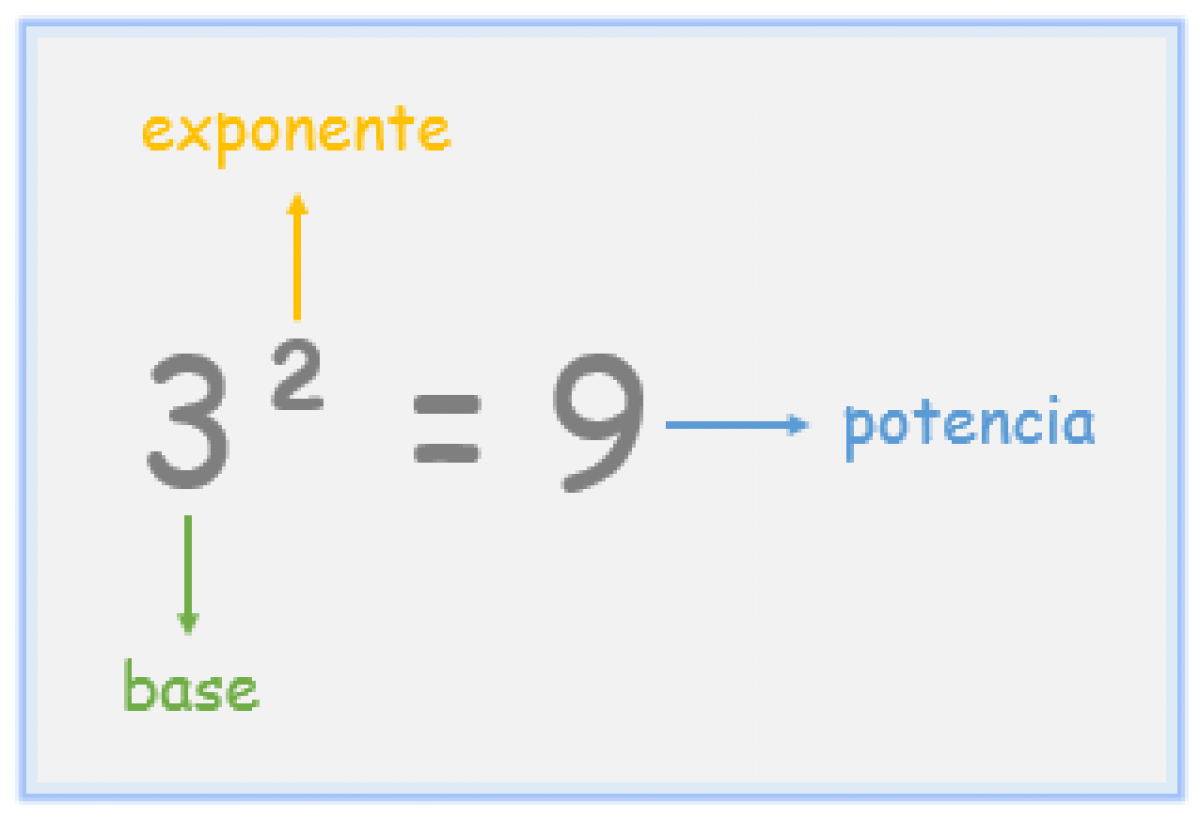
operación matemática que consiste en repetir un número llamado base tantas veces como factor, como lo indica otro llamado exponente; al resultado de esta operación se le denomina
potencia.
EJEMPLO (IMAGEN 8)
Radicación
operación que consiste en hacer corresponder dos números llamados índice y radicando con un tercer número llamado raíz, el cuál es único en R.
EJEMPLO (IMAGEN 7)
Leyes de exponentes
conjunto de definiciones y teoremas que estudian a las diferentes relaciones, operaciones
y transformaciones que se pueden realizar con los exponentes.
como por ejemplo:
Producto de potencias de igual base
Cociente de potencias de igual base
Potencia de exponente cero
Potencia de una potencia
Raíz de una potencia
FRACCIONES ALGEBRAICAS RACIONALES
Operaciones con fracciones
sumar o restar fracciones es necesario hallar el mínimo común múltiplo de los denominadores.
multiplicar fracciones se multiplican numeradores y denominadores entre si.
dividir fracciones se invierte la fracción del divisor y se procede como en la multiplicación.
Simplificación de fracciones
Simplificar una fracción es transformarla en otra equivalente e irreductible.
EJEMPLO (IMAGEN 6)
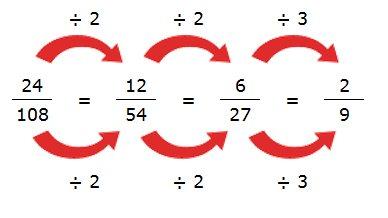
Signos de una fracción
Toda fracción posee tres signos : signo del numerador, signo del denominador y signo de la
fracción. El cambio de dos signos de una fracción no altera el signo total de la fracción
Clases de fracciones
Existen las siguientes
Fracción propia
Se caracteriza porque el grado del numerador es menor que el grado del denominador
Fracción impropia
Se caracteriza porque el grado del numerador es mayor o igual que el grado del denominador
Fracciónes Homogeneas
Son fracciones que tienen el mismo denominador
Fracción Heterogeneas
Son fracciones que tienen diferente denominador
Fracciones equivalentes
Son aquellas que teniendo formas diferentes se caracterizan porque siempre tendrán los mismos valores numéricos, para cualquier valor asignado a sus variables, a excepción de aquellos que hagan cero el denominador.
Fracciones complejas o compuestas
Se caracterizan porque en su numerador o denominador, o en ambos, aparecen otras
fracciones algebraicas.
Fracciones continuas
Es un caso particular de las fracciones complejas, que se caracterizan porque en el numerador
de cada fracción siempre esta la unidad.
Fracción irreductible
Son aquellas fracciones que se caracterizan porque en el numerador y denominador aparecen
expresiones que no tienen ningún factor común, es decir no admiten simplificación.
ES
el cociente indicado de dos expresiones algebraicas racionales en
donde al menos una letra o variable figura en el denominador.
EJEMPLO (IMAGEN 5)

FACTORIZACIÓN
ES
la transformación de un polinomio en una multiplicación indicada de dos o mas
polinomios primos dentro de cierto campo de números
Métodos para factorizar una expresión algebraica
A. Método de factor común
B. Método de identidades
C. Método del aspa simple
D. Regla de Ruffini
E. Método de los artificios:
a) Cambio de variable o agrupaciones convenientes
b) Quita y pon o reducción a diferencia de cuadrados
c) Sumas y restas especiales
ES
Se conoce como álgebra a la rama de la matemática en la cual las operaciones son generalizadas empleando números, letras y signos que representan simbólicamente un número u otra entidad matemática.

Según Baldor (IMAGEN 1)
álgebra es la rama de la matemática que estudia la cantidad considerada del modo más general posible.
EXPRESIONES ALGEBRAICAS
ES
Una combinación de números y letras (variables) unidas entre sí por los signos de diferentes operaciones aritméticas: adición, sustracción,
multiplicación, división, potenciación y radicación en una cantidad limitada de veces.
EJEMPLO
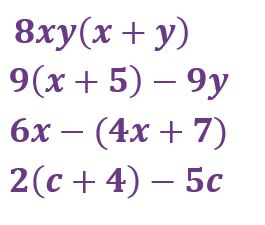
CLASIFICACIÓN
POR SU FORMA O NATURALEZA Se clasifican de acuerdo a la forma de sus exponentes que afectan a sus variables.
Expresión algebraica racional
cuando los exponentes de la parte literal( letras) son números enteros.
Expresión algebraica racional entera: se caracteriza por presentar exponentes enteros positivos en su parte literal; es decir, no tiene parte literal en su denominador.
Expresión algebraica racional fraccionaria: se caracteriza por presentar exponentes negativos en su parte literal; es decir, tiene parte literal en su denominador.
Expresión algebraica irracional
cuando presenta exponentes fraccionarios en su parte
literal.
POR SU NUMERO DE TERMINOS
Monomio
Es una expresión algebraica que consta de un sólo término.
Multinomio
Es una expresión algebraica que consta de dos o más términos algebraicos.
IMAGEN 2
GRADO DE UNA EXPRESIÓN ALGEBRAICA
Grado de un monomio
- Grado absoluto: está dado por la suma de los exponentes de todas sus letras.
- Grado relativo: está dado por el exponente de la letra referida.
Grado de un polinomio
- Grado absoluto: está dado por el monomio de mayor grado absoluto.
- Grado relativo: está dado por el mayor exponente de la letra referida.
VALOR NUMERICO DE LAS EXPRESEIONES
Resultado de sustituir cada una de
las letras(variables) por números y realizar las operaciones indicadas.
OPERACIONES CON POLINOMIOS ENTEROS
Adición y sustracción de polinomios
ADICIÓN
es una operación que tiene por objeto reunir dos o mas polinomios (sumandos) en una sola expresión( suma)
SUSTRACIÓN
es la operación que consiste en sumar al polinomio minuendo el
opuesto del polinomio sustraendo para obtener el polinomio diferencia.undefined
Multiplicación de polinomios
ES
la operación que consiste en obtener una expresión llamada producto, conociendo otras dos llamadas multiplicando y multiplicador.
EJEMPLO (IMAGEN 3)
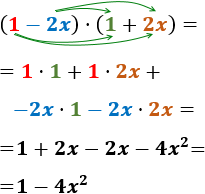
Productos notables
SON
productos indicados que tienen una forma determinada, de los cuales se puede recordar
fácilmente su desarrollo sin necesidad de efectuar la operación.
LO MAS IMPORTANTES SON
Binomio al cuadrado
Trinomio al cuadrado
Binomio al cubo
Diferencia de cuadrados
Diferencia de cubos
Identidad de ARGAND
Producto de binomios con un término común
Producto de binomios de la forma (ax + b)(cx + d )
Identidades de Legendre
Identidades de Lagrange
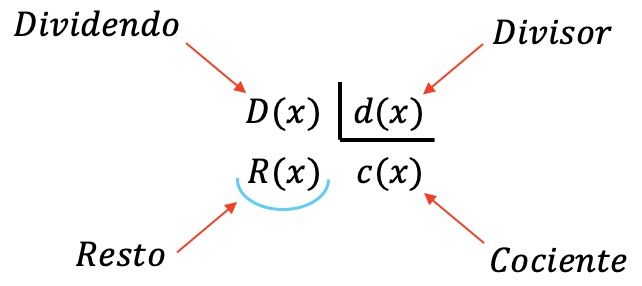
División de polinomios
ES
una operación que consiste en hallar el polinomio cociente dados el polinomio dividendo y el polinomio divisor.
EJEMPLO (IMAGEN 4)