Aplicaciones de la derivada al análisis de funciones.

El crecimiento y decrecimiento de una función f se puede estudiar en un intervalo [a,b], en un punto x o en todo el dominio.

Funcion Creciente

• Cuando al incrementarse el valor de la variable independiente (x), se incrementa también el valor de la variable dependiente f(x). • Dada la función "f" y los valores: X1 y X2 del dominio, sera creciente si: x1<x2 = f(x1)<f(x2)

EJEMPLO

Funcion Decreciente

• Cuando al incrementarse la variable independiente (x) disminuye el valor de la variable dependiente f(x). •Dada una función "f" y los valores: X1 y X2 del dominio, sera decreciente si: x1>x2 = f(x1)>f(x2)

EJEMPLO

Un punto de inflexión, en una función matemática, es un punto donde los valores de una función continua en x pasan de un tipo de concavidad a otra. La curva "atraviesa" la tangente.Matemáticamente la derivada segunda de la función f en el punto de inflexión es cero,o no existe.

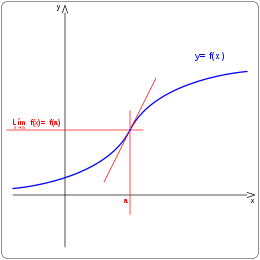
TEOREMA

Sea la ecuación de una función.
Si no existe, y la derivada cambia de signo al pasar por el valor de x=a, entonces, el punto de la función de abscisa x=a es un punto de inflexión.

EJEMPLO

f(x)=x3-3x2+6x-6 ; f(x)=3x2-6x+6 ; f(x)=6x-6 f(x)=0 ; 6x-6=0 = x=1 El punto x=1 es un punto de inflexión, puesto que antes de x=1 la derivada segunda es negativa (convexa) y después de x=1 es positiva (cóncava).

Si f : u ⊂ Rn → R es una función escalar, dado un punto x0 ∈ u se llama mínimo local de f si existe una vecindad v de x0 tal que ∀ x ∈ v f(x) ≥ f(x0). De manera análoga, x0 ∈ u es un máximo local si existe una vecindad v de x0 tal que f(x) < f(x0) ∀ x ∈ v. El punto x0 ∈ u es un extremo local o relativo, si es un mínimo local o máximo
local.

EJEMPLO

Hallar los máximos y mínimos de la función f : R2 → R, definida por f(x, y) =x2 + y2 − 2x − 6y + 14
Solución: Debemos identificar los puntos críticos de f resolviendo fx = 0, fy = 0 para x, y, fx = 2x − 2, fy = 2y − 6. De modo que el punto critico es (1, 3).Como: f(x, y) = (x2 − 2x + 1) + (y2 − 6y + 9) + 4 = (x − 1)2 + (y − 3)2 + 4
tenemos que f(x, y) ≥ 4 por lo tanto en (1, 3) f alcanza un mínimo relativo.

TEOREMA

Para que una función derivable en x0 tenga un extremo local en x0 es necesario que se cumpla f ‘(x0)=0.
Como el crecimiento está determinado por el signo de la derivada tenemos:
x0 es un punto de

•Máximo local si f ‘(x) pasa de positiva a negativa.
•Mínimo local si f ‘(x) pasa de negativa a positiva.

Concavidad

Una función es CÓNCAVA o presenta su concavidad hacia abajo cuando dados dos puntos cualesquiera el segmento que los une queda por debajo de la curva.

EJEMPLO

Convexidad

Una funcion es CONVEXA o presenta su concavidad hacia arriba si dados dos puntos de la curva el segmento que los une queda por encima de la curva.

EJEMPLO