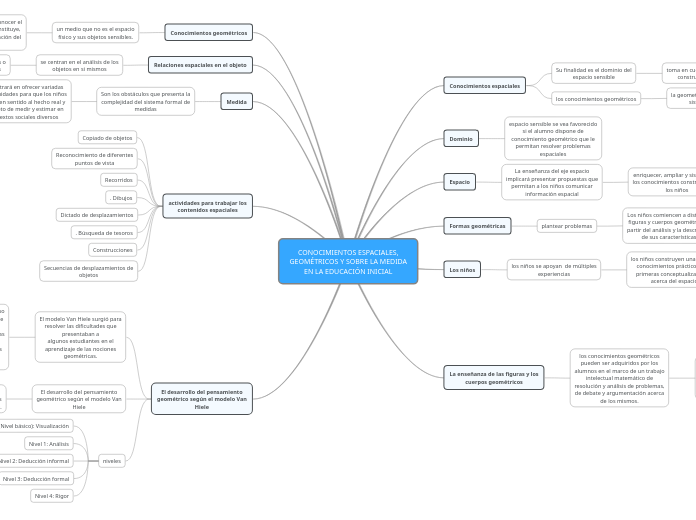
CONOCIMIENTOS ESPACIALES,
GEOMÉTRICOS Y SOBRE LA MEDIDA
EN LA EDUCACIÓN INICIAL
Conocimientos espaciales
Su finalidad es el dominio del
espacio sensible
toma en cuenta acciones como
construir, desplazarse.
acciones de comunicación de esas
acciones o sus comprobaciones
los conocimientos geométricos
la geometría debe ser enseñada
sistemáticamente.
Dominio
espacio sensible se vea favorecido
si el alumno dispone de
conocimiento geométrico que le
permitan resolver problemas
espaciales
Espacio
La enseñanza del eje espacio
implicará presentar propuestas que
permitan a los niños comunicar
información espacial
enriquecer, ampliar y sistematizar
los conocimientos construidos por
los niños
en el entorno
extraescolar, mediante la
expansión del dominio de
experiencias espaciales
Formas geométricas
plantear problemas
Los niños comiencen a distinguir
figuras y cuerpos geométricos a
partir del análisis y la descripción
de sus características;
La posibilidad de nombrar figuras
o cuerpos, como también algunos
de sus elementos tales como lados
rectos, curvos, caras planas y
vértices
Los niños
los niños se apoyan de múltiples
experiencias
los niños construyen una serie de
conocimientos prácticos y las
primeras conceptualizaciones
acerca del espacio
resuleven problemas, en las
decisiones respecto de qué hacer
frente a ese problema
La enseñanza de las figuras y los
cuerpos geométricos
los conocimientos geométricos
pueden ser adquiridos por los
alumnos en el marco de un trabajo
intelectual matemático de
resolución y análisis de problemas,
de debate y argumentación acerca
de los mismos.
Este “modo de pensar” supone
apoyarse en los conocimientos que
se disponen para anticipar
relaciones no conocidas o inferir
nuevas propiedade
Integra situaciones como
. Observación de objetos
geométricos
Clasificaciones
Representaciones gráficas
Situaciones de pedidos
Copia de un objeto tridimensional
Copia de un espacio bidimensional
Construcción y reproducción de
guardas
Dictado de figuras
Tangram - Puzzles geométricos
Conocimientos geométricos
un medio que no es el espacio
físico y sus objetos sensibles.
permite comprender y conocer el
espacio sensible y se constituye,
en parte, como modelización del
espacio físico.
es
las conceptualizaciones que el niño
tiene del mismo, a través de su
saber matemático
Relaciones espaciales en el objeto
se centran en el análisis de los
objetos en si mismos
caras, vértices, tipo de lados o
caras en cuerpos y figuras
Medida
Son los obstáculos que presenta la
complejidad del sistema formal de
medidas
se centrará en ofrecer variadas
oportunidades para que los niños
otorguen sentido al hecho real y
concreto de medir y estimar en
contextos sociales diversos
actividades para trabajar los
contenidos espaciales
Copiado de objetos
Reconocimiento de diferentes
puntos de vista
Recorridos
. Dibujos
Dictado de desplazamientos
. Búsqueda de tesoros
Construcciones
Secuencias de desplazamientos de
objetos
El desarrollo del pensamiento
geométrico según el modelo Van
Hiele
El modelo Van Hiele surgió para
resolver las dificultades que
presentaban a
algunos estudiantes en el
aprendizaje de las nociones
geométricas.
se construye a partir de un proceso
que sigue una lenta evolución que
va desde las formas intuitivas
iniciales del pensamiento, hasta las
formas deductivas finales, que
corresponden a niveles escolares
superiores. Esta secuencia
atraviesa cinco niveles.
Secuencial
Carácter del progreso
Relación entre los niveles
Lenguaje
Desajuste
El desarrollo del pensamiento
geométrico según el modelo Van
Hiele
debe incluir contenidos
relacionados con las formas, es
decir, con los cuerpos y figuras.
niveles
Nivel 0 (Nivel básico): Visualización
Nivel 1: Análisis
Nivel 2: Deducción informal
Nivel 3: Deducción formal
Nivel 4: Rigor