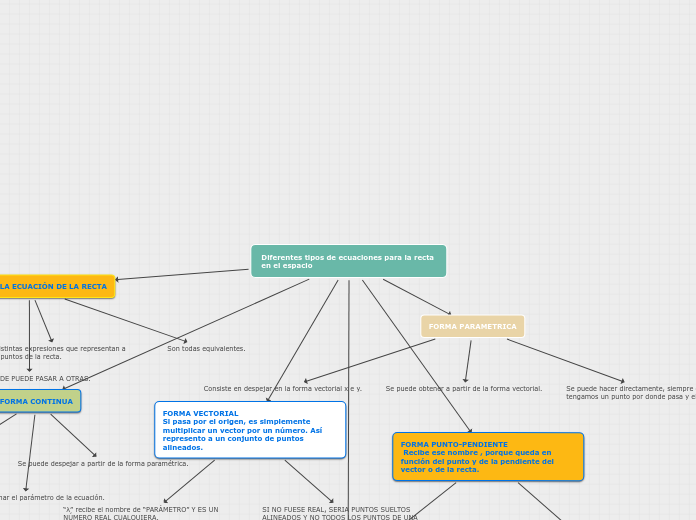
Diferentes tipos de ecuaciones para la recta en el espacio

FORMAS DE LA ECUACIÓN DE LA RECTA

Son las distintas expresiones que representan a todos los puntos de la recta.

Son todas equivalentes.

DE UNAS DE PUEDE PASAR A OTRAS.

FORMA VECTORIAL
Si pasa por el origen, es simplemente multiplicar un vector por un número. Así represento a un conjunto de puntos alineados.

“λ” recibe el nombre de “PARÁMETRO” Y ES UN NÚMERO REAL CUALQUIERA.

SI NO FUESE REAL, SERIA PUNTOS SUELTOS ALINEADOS Y NO TODOS LOS PUNTOS DE UNA RECTA.

FORMA PARAMETRICA

Consiste en despejar en la forma vectorial x e y.

Se puede obtener a partir de la forma vectorial.

Se puede hacer directamente, siempre que tengamos un punto por donde pasa y el vector.

FORMA CONTINUA

Se trata de eliminar el parámetro de la ecuación.

Se puede construir directamente.

Se puede despejar a partir de la forma paramétrica.

FORMA PUNTO-PENDIENTE
Recibe ese nombre , porque queda en función del punto y de la pendiente del vector o de la recta.

Al coeficiente de x, es la pendiente de la recta y se representa por m.

La pendiente de una recta es igual a la tangente del ángulo que forma la recta o el vector con el eje de abscisas, medido en sentido contrario a las agujas del reloj y desde el eje OX positivo.

FORMA GENERAL, Se trata de dejar una ecuación, con dos variables e igualada a cero

Lo fundamental de la forma general es que es la manera idónea de tener una recta para resolver un sistema con otra y ver su punto de corte.

Otro punto importante es que los coeficientes de las variables forman un vector perpendicular a la recta.

(A, B) es un vector perpendicular a la recta, por tanto el vector de la recta es (B, -A).