
Enseñar a pensar matemáticamente
Creando espacios para el Pensamiento creativo

Convergente y divergente
Convergente

Principio de la no contradicción
Divergente

Creador
Utilizando los métodos
HEURÍSITICA DE PÓLYA

Resolución de un problema
1. Entender el problema
Clasificar
Incógnita
condición
Datos
2.confeccionar una estrategia de solución
3.Desarrollar el problema
4.Volver al problema, la respuesta y el método de solución.
Docente establece un segundo modelo para orientar una discusión
Resolución de problemas según: Schoenfeld
Recursos
Concimientos Previos
conceptos
procedimientos
fórmulas
Heurística
Estrategias
Técnicas
Control o metacognición
Creencias
Favorables
Desfavorables
CIENTÍFICO
1.Observando cuidadosamente el fenómeno
2. Inducción o extracción a partir de la observación o experimentación
3. Hipótesis o planteamiento
4. Comprobación de las hipótesis
5.Demostración o refutación de la hipótesis
6. Tesis o conclusión
Planteando Situaciones problémicas
Interacción

estudiantes y docente

Objetos de conocimiento matemático
Que debe:
1. involucrar implícitamente los conceptos que se va a aprender
2. Ser enunciado de un verdadero problema
3. Ser accesible a la mentalidad estudiantil
4. Permitir la utilización de conocimientos previos
Translado al aula
Lo que se desea: Redescubrimiento de conceptos y relaciones
Aprendizaje significativo
Formulación del problema
Análisis del problema
facilitando
Comunicación oral
Lectura analítica
Planeador de clase
1. Preparar al estudiante para seguir instrucciones
psicológicamente
Prácticamente
2. Familiarizar al estudiante con la forma de desarrollar actividades

trabajo en conjunto con el profesor
Prepara sesiones no muy largas
Graduar la adaptación
3. Dar entrada al proceso de lectura y escritura
Orden de actividades
1. de entrenamiento

Capacidad de comprensión de las situaciones
Cómo se crear:
1. Decir lo mismo pero con diferentes palabras
2. Separar los datos y las incógnitas
3. Deducir qué se puede calcular a partir de unos datos conocidos
2. De reconocimiento y aplicación de fases
Comprensión
Planificación
Ejecución
Comprobación del resultado
3. si hay dificultades
El docente expresará verbalmente
las diferentes fases con
pensamientos
razonamiento
Procesos mentales
al inicio y hasta terminar la resolución
Sesiones más largas
Adopción de protagonismo
Utilizando herramientas tecnológicas
Incrementando el uso de
calculadoras
computador
Clases de problemas con las que cuenta el docente
Ecuaciones de segundo grado
La razón Áurea
utilizando el método de factorización
Solución geométrica de la ecuación
Ecuaciones con tres incógnitas
Se debe iniciar su análisis
Donde sea fácil eliminar una de las variables
Mediante la ejecución combinada de
operaciones algebraicas elementales
Adición
Sustracción
Ecuaciones con dos incógnitas
Desarrollar habilidades
a través de la aplicación
De control de variables
Problemas de ecuaciones lineales con una incógnita
Situaciones problémicas
Problemas sobre áreas y perímetros
Utilizando regla y compás
Construir segmentos
longitudes
Raíz cuadrada
Cociente
producto
diferencia
suma
Análisis de la ecuación
Ecuaciones con una incógnita
Modelos matemáticos
Utilzando
Reglas de cuisenaire
Enseñanza
Teoremas
Demostraciones
Capacidad para entender y apreciar
Conceptos abstractos
Abstracciones simbólicas del álgebra

Pensamiento formal
Características
Funcionales
enfoques y estrategias para abordar problemas
Carácter hipotético deductivo y proposicional
Estructurales
sirven para formalizar el pensamiento
Establece hipótesis
Uitiliza
Conjunción
Disyunción
Implicación
equivalencia
Negación

Desarrollo humano pensamiento lógico inductivo y deductivo
Proceso de Asimilación Desarrollo próximo
Relación entre el aprendiz y el experto
Nivel 1
Ayuda de otros

familiares, maestros, condíscipulos
Nivel 2
Ayuda del mismo sujeto
Acceder, procesar la información
Visulaizar, resolver problemas
Explorar y verificar conjeturas
Verificar soluciones
Reconstruida, reconquistada o redescubierta la verdad
Reacomodo
Entre el segundo y tercer nivel
Desequlibrio
Nivel 3
Nuevos Conceptos
Interiorización
Automatización
Fijación
Nivel 4
Desautomatización
Recurrencia a los niveles anteriores
Problemas aritméticos
Datos expresados en decimales, fracciones o porcentuales Tercer nivel
Regla de tres
Directa
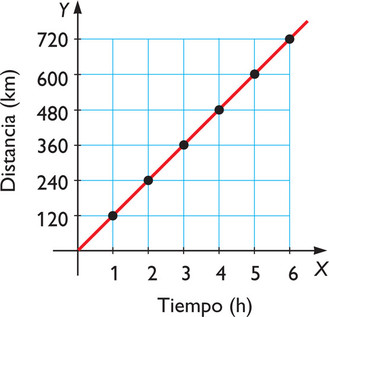
Cantidades aumenta o disminuyen en la misma proporción
Inversa

Una cantidad aumenta y la otra disminuye o viceversa
Proporción
Igualdad entre dos razones
Primer actividad
Relacionando medidas diferentes
Producto de los extremos= Producto de los medios
Razón
Par ordenado de números usados para establecer comparación entre las cantidades que representen.
Comparan unidades diferentes
Porcentaje
Hallar
cantidades
Resultante al efectuar un aumento o disminución porcentual
Un tanto porciento
Son de tres clases
1.Se conoce el Porcentaje de la unidad y la parte de la otra
Se debe hallar el total de la otra parte
2.Se conoce el porcentaje de la unidad y el total de la otra
Se debe hallar esa parte
3. Se conoce el total y la parte de la segunda unidad
Se desea conocer la parte del porcentaje
Fracciones
Comparan partes en con relación a un todo
Estrategia
Modelo conjuntista
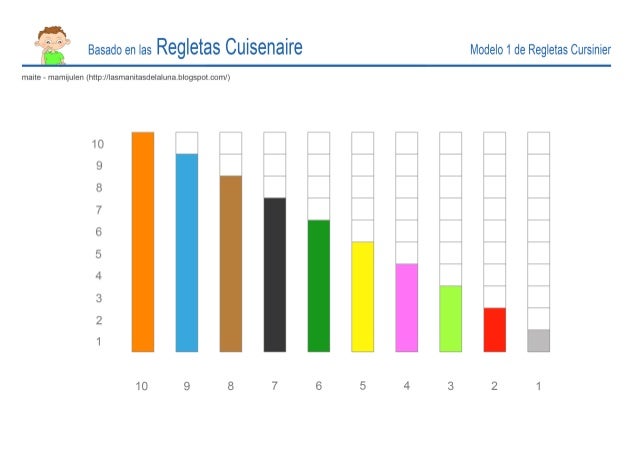
Regletas de Cuisenaire
Inducen el concepto de mínimo común múltiplo
actividades de ensayo y error
Datos expresados en decimales, fracciones o porcentuales
Segundo nivel
Análisis de situaciones como herramienta heurística
Establecer igualdad
Interpretar mediante igualdades númericas oraciones
problemas combinados la suma o resta con la multiplicación o la división
Problemas indirectos
Se deben ordenar
En función de una pregunta clave
Problemas directos
Orden lógico
Datos
Problemas combinados mixtos
Campos conceptuales diferentes
Descubrir
Plan de solución
Ordenando de una estructura a la otra
Relaciones aditivas y multiplicativas
Subtema
Problemas combinados puros
Mismo campo Operativo conceptual
Multiplicación-División
Adición-sustracción
Problemas combinados fraccionados
Incluyen al final del texto dos o más preguntas concatenadas
Suma de problemas de primer nivel
Primer nivel
Mutiplicación-división
Problemas heurísticos con la relación entre la adición y la multiplicación
Problemas que se pueden proponer
familia de un natural
Plantear situaciones problémicas a partir de de una igualdad
Utilizando expresiones como mayor o menor
contexto de igualdades en diferentes situaciones
Diferencias aritméticas teniendo en cuenta el orden de la escritura
planeando situaciones de suma o diferencia utilizando el cero
Nunca anunciar la propiedad modulativa de la suma
Extender las familias numéricas a cantidades de dos cifras
Pedir a los estudiantes que agrupen los asociados por parejas
asociados por diferencia
Descubrir relaciones
Pidiendo que resuelva interrogantes con
Asociaciones y valor posicional
Definición de diferencia
Comparando cantidades y resolviendo igualdades
Utilizando las regletas de Cuisenaire

Utilizando la calculadora para verificar
Comparando resultado con el símbolo + y x
Utilizando


Tablero de las tiras de suma de Montessori
Propiedad del producto
Asociativa
Distributiva
conmutativa
Se clasifican en
De razón
medida de tres magnitudes
Comparación multiplicativa
Cuantificadores
Veces más que
Veces menos que
Repartos equitativos
repartirse en grupos iguales
situaciones
1. cantidad que se reparte ?
operación es un producto
2. número de elementos por cada grupo ?
operación división
3 númerr de grupos ?.
operación división
Clases de producto
Sumandos iguales
Dos conjuntos diferentes
Producto de medidas
Producto cartesiano
Aditivo-sustractivos
Problemas heuríticos con la suma
Estrategias
Propiedad conmutativa y asociativa de la adición
Plantear situaciones problémicas fáciles de solucionar
1. Planear una operación algorítmica completando una igualdad que a partir de ella se establece una diferencia.
2. Con estos datos se puede proceder a plantear problemas y dar solución a ellos
Problemas de clase parte-parte-total
C1+C2=Conjunto total Relación de conjuntos
Una parte desconocida
CT-C2=C1
Ct-C1=C2
Total desconocido
C1+ C2= Ct ?

Problemas de comparación entre dos cantidades
Ser mayor que
Ser menor que

Problemas de igualación
Tantos como, igual que
Problemas de cambio Cantidad inicial+modificación =Cantidad final
Cantidad inicial es mayor Disgregación
C inicial- Modificación ?= C final
C inicial? =C final+Modificación
C inicial- Modificación= C final ?
Cantidad final es mayor reunión o agregado
C inicial+Modificación=C final ?
C inicial+ modificación ?= C final
C final- C inicial=Modificación
C inicial ? + modificación =C final
C final -Modificación =C inicial

