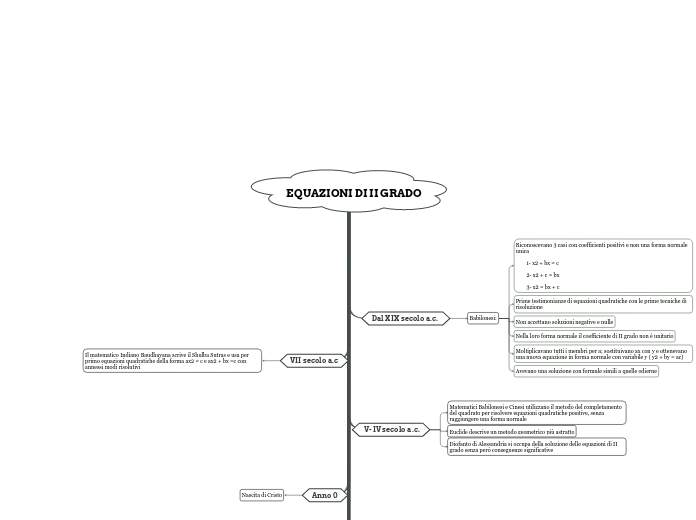
EQUAZIONI DI II GRADO
Dal XIX secolo a.c.
Babilonesi:
Riconoscevano 3 casi con coefficienti positivi e non una forma normale unica
1- x2 + bx = c
2- x2 + c = bx
3- x2 = bx + c
Prime testimonianze di equazioni quadratiche con le prime tecniche di risoluzione
Non accettano soluzioni negative e nulle
Nella loro forma normale il coefficiente di II grado non è unitario
Moltiplicavano tutti i membri per a; sostituivano ax con y e ottenevano una nuova equazione in forma normale con variabile y ( y2 + by = ac)
Avevano una soluzione con formule simili a quelle odierne
V- IV secolo a.c.
Matematici Babilonesi e Cinesi utilizzano il metodo del completamento del quadrato per risolvere equazioni quadratiche positive, senza raggiungere una forma normale
Diofanto di Alessandria si occupa della soluzione delle equazioni di II grado senza però conseguenze significative
VII secolo a.c
Il matematico Indiano Baudhayana scrive il Shulba Sutras e usa per primo equazioni quadratiche della forma ax2 = c e ax2 + bx =c con annessi modi risolutivi
Anno 0
Nascita di Cristo
Dal II al IV secolo d.c.
Stesura manoscritto Bakhshali, con la formula risolutiva delle equazioni quadratiche
Dal IX al X secolo d.c.
Al-Khwarizmi:
Sviluppa un insieme di formule che funzionava per soluzioni positive
Distingue 5 tipi di equazioni ( le tre dei babilonesi e l'equazione PURA x2 = c e quella SPURIA x2 = bx )
Soluzioni negative non accettate
Utilizza il metodo del completamento del quadrato proponendo anche una trasposizione grafica
Riconosciuto a SRIDHAra la priorità della scoperta della formula generale per risolvere un'equazione quadratica
Abraham bar Hiyya Ha-Nasi introduce per la prima volta in Europa la soluzione completa con il suo Liber embadorum
XVI secolo d.c
Viete:
Introduce le lettere per esprimere i coefficienti dell'equazione
Scopre formule che mettono in relazione i coefficienti dell'equazione con le radici
Data
VII secolo d.c.
Brahmagupta, I° matematico noto ad aver usato la formula algebrica generale, consentendo soluzioni positive e negative
XV secolo d.c.
Si iniziano ad accettare soluzioni negative, complesse e si inizia a porre l'equazione in un'unica forma normale
XVIII secolo d.c.
Cartesio introduce la regola dei segni