Es una agrupación, clase o colección de objetos denominados elementos del conjunto.
NOTACIÓN:Son cada uno de los elementos que hacen parte de un conjunto y que se caracterizan por tener una cualidad individual que nos permiten diferenciarlos uno del otro.
Comprensión:Un conjunto está determinado por compresión cuando solamente se menciona una característica común de todos los elementos. Ejemplo: B = {vocales} o B = {x / x es volcal}
Extensión:Un conjunto está determinado por extensión cuando se escriben uno a uno todos sus elementos A = {a, e, i, o, u}
OPERACIONES CON CONJUNTOS
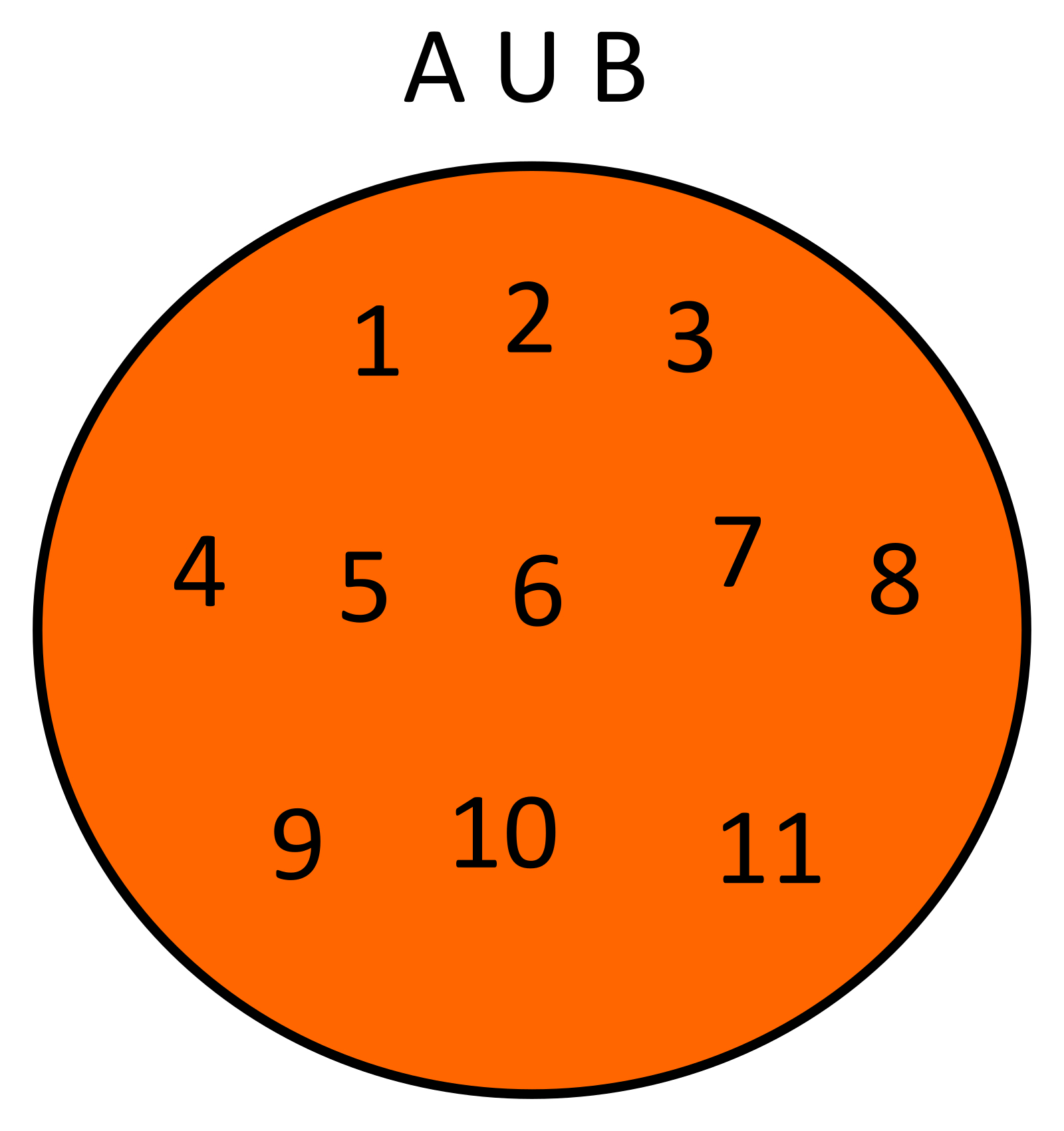
UNIÓN:Es la operación que nos permite unir dos o más conjuntos para formar otro conjunto que contendrá a todos los elementos que queremos unir pero sin que se repitan. Ejemplo Dados dos conjuntos A={1,2,3,4,5,6,7,} y B={8,9,10,11} la unión de estos conjuntos será A∪B={1,2,3,4,5,6,7,8,9,10,11}:
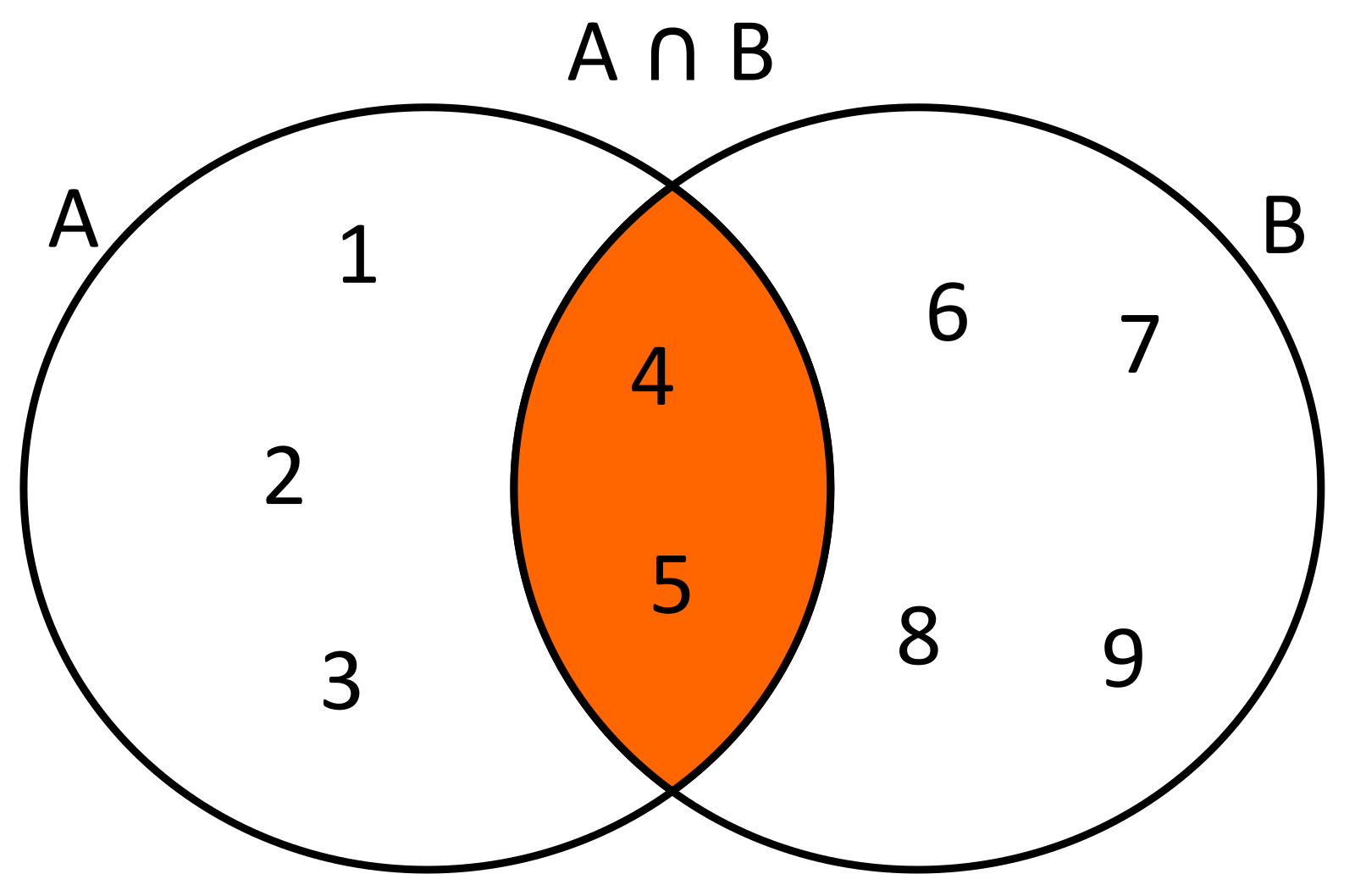
INTERSECCIÓN:Es la operación que nos permite formar un conjunto, sólo con los elementos comunes involucrados en la operación Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la intersección de estos conjuntos será A∩B={4,5}.
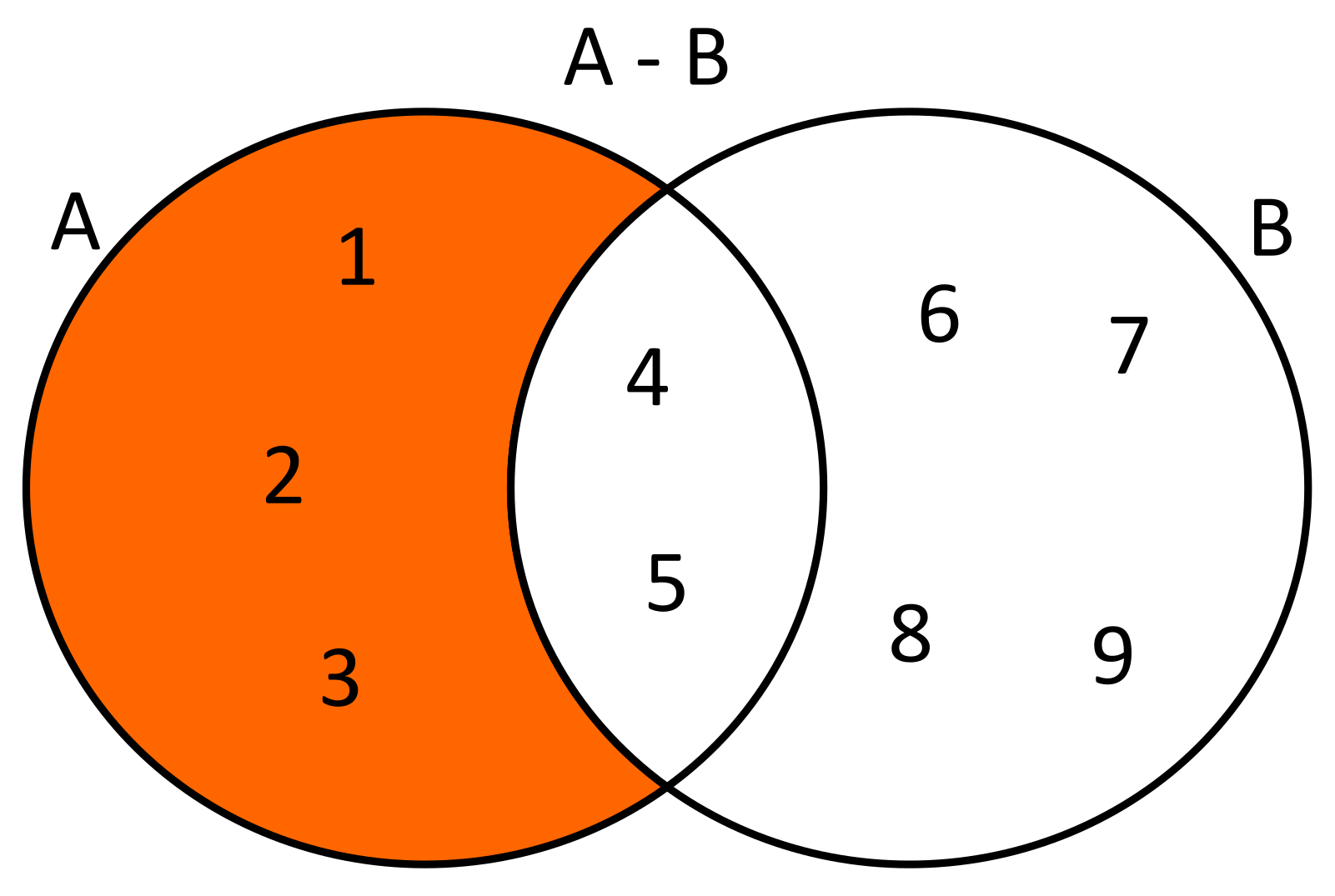
DIFERENCIA: Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que pertenecen al primero pero no al segundo. Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia de estos conjuntos será A-B={1,2,3}
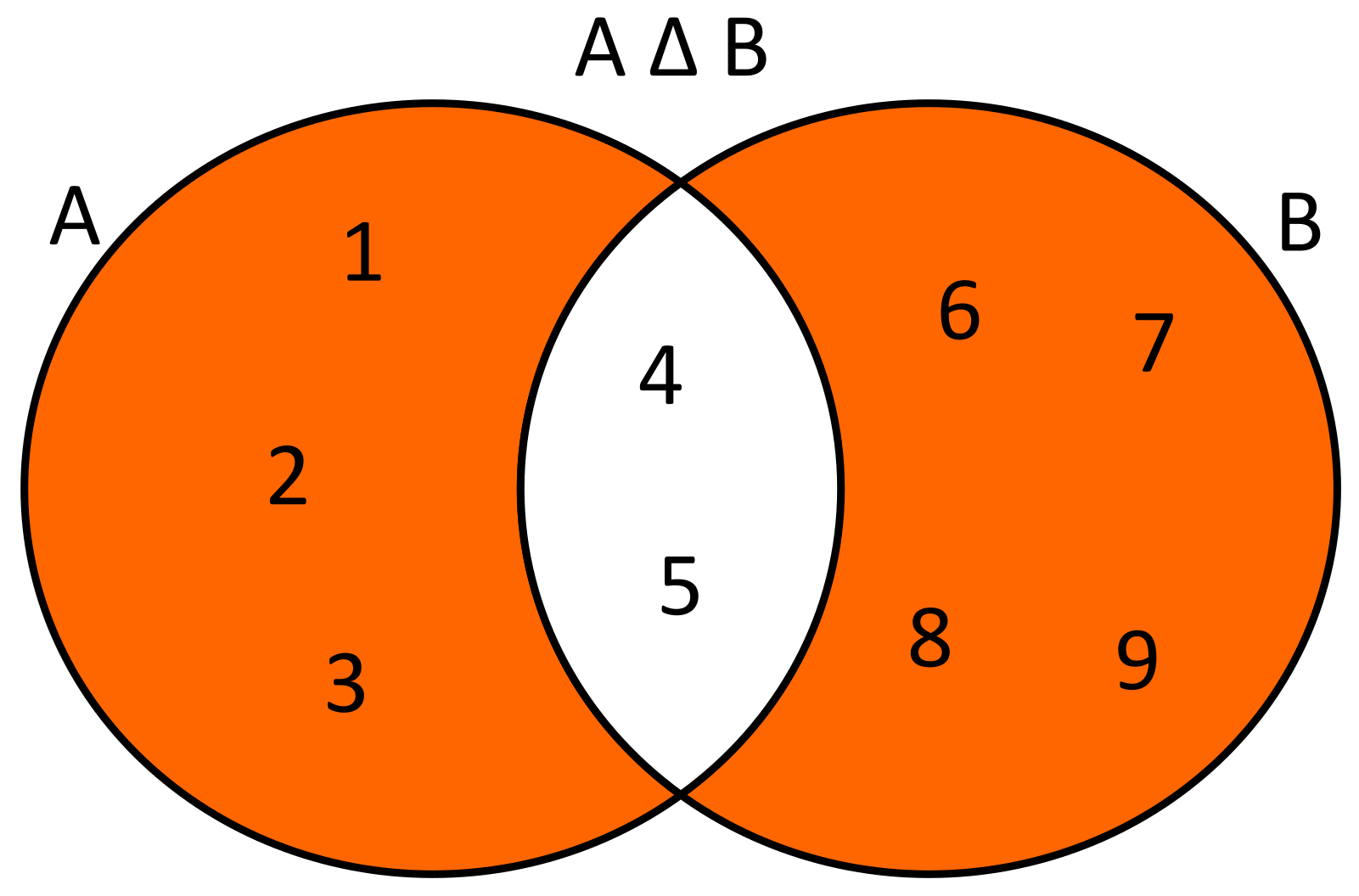
DIFERENCIA DE SIMÉTRICA: Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que no sean comunes a ambos conjuntos Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia simétrica de estos conjuntos será A △ B={1,2,3,6,7,8,9}.
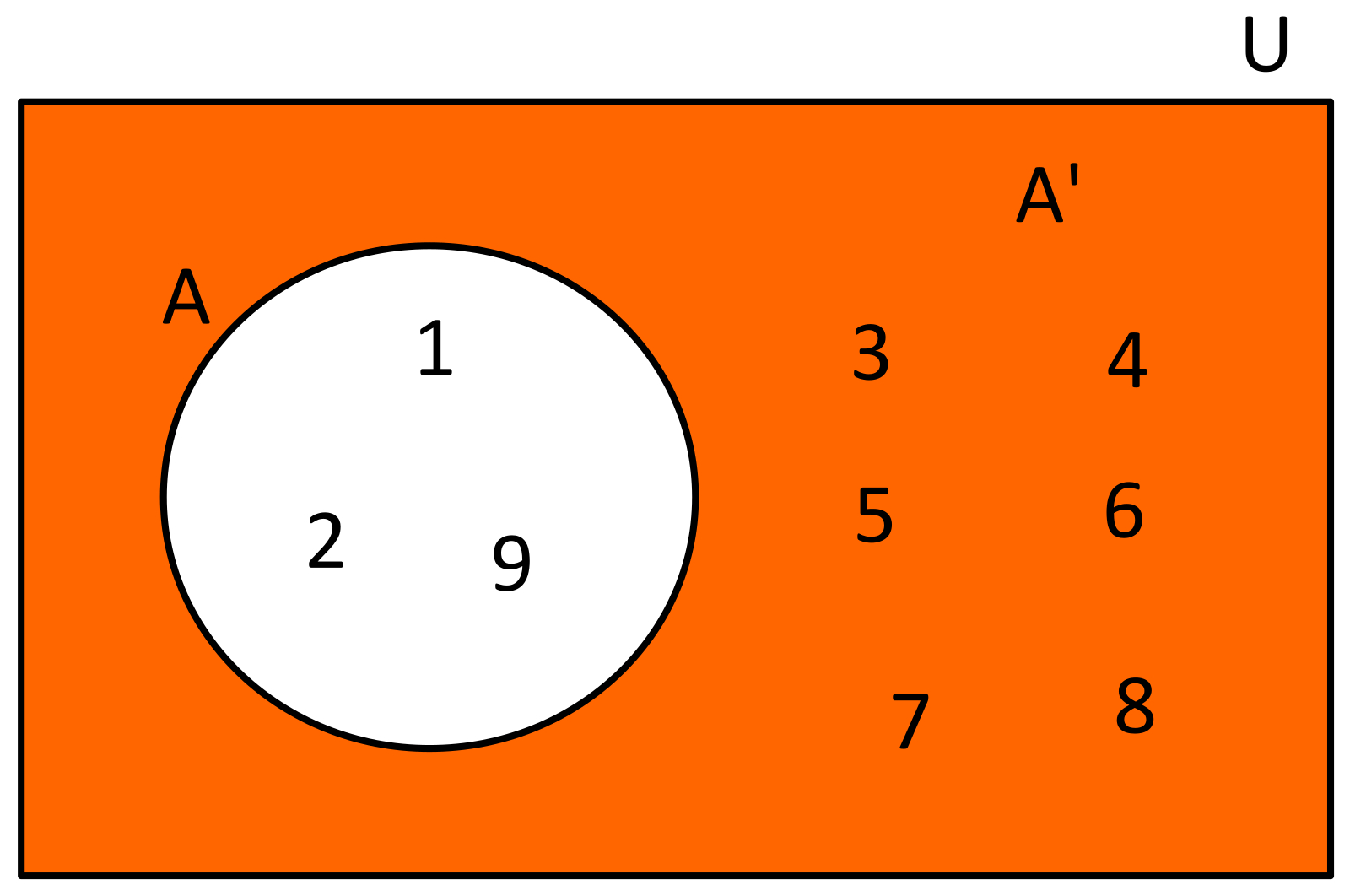
COMPLEMENTO: Es la operación que nos permite formar un conjunto con todos los elementos del conjunto de referencia o universal, que no están en el conjunto. U={1,2,3,4,5,6,7,8,9} y el conjunto A={1,2,9}, el conjunto A' estará formado por los siguientes elementos A'={3,4,5,6,7,8}.
TIPOS DE CONJUNTOS:
IGUALDAD DE CONJUNTOS:Conjuntos Iguales son aquellos conjuntos que tienen exactamente los mismos elementos. A = {rojo, amarillo, azul}
B = {azul, rojo, amarillo}
Dos conjuntos A y B son iguales si. A⊂ B y B⊂A
SUBCONJUNTOS: Un subconjunto de un conjunto A es aquel conjunto que está formado por un grupo de elementos de A.
Un conjunto A que es subconjunto de B se representa como:
A ⊂ B
CONJUNTO VACÍO: El conjunto que no contiene elementos. Esto se denomina conjunto vacío o nulo, se denota con el símbolo ∅.
CONJUNTOS DISJUNTOS: Se definen los conjuntos disjuntos como aquellos conjuntos que no tienen elementos en común.
A, B son conjuntos disjuntos si ∈ A → x ∉ B y x ∈ A → x ∉ B
Dos conjuntos disjuntos A y B tienen la siguiente propiedad: A ∩ B = ∅