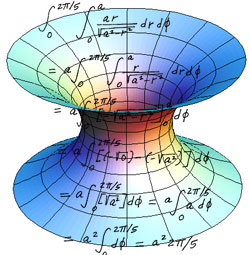
Funciones, Modelos Y Limites
LIMITES
CONCEPTO
En el cálculo a menudo se desea conocer el valor del límite de una función a medida que la variable independiente se aproxima a un número real específico. Este valor límite, cuando existe, recibe el nombre de límite.
MODELOS
PROPIEDADES Y CONTINUIDAD

LIMITES DETERMINADOS E INDETERMINADOS
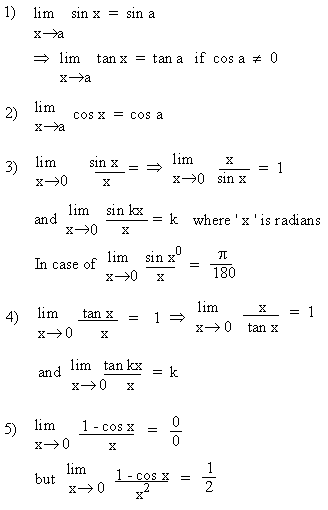
LIMITES ESPECIALES

LIMITES AL INFINITO
FUNCIONES
El concepto de función retoma conocimientos básicos de matemáticas transformándolos en una estructura, la cual es base del cálculo. Este concepto se ocupa de relacionar cada uno de los elementos de un conjunto con elementos de otro. f: A → B
MODELOS
REPRESENTACION DE UNA FUNCIÓN

GRÁFICA
ANALÍTICA

SAGITAL
DOMINIO
DETERMINACIÓN DE DOMINIO
CLASIFICACIÓN DE FUNCIONES

TRASCENDENTES
ALGEBRAICAS
IDENTIDAD

LINEAL

CUADRATICA

CONSTANTE
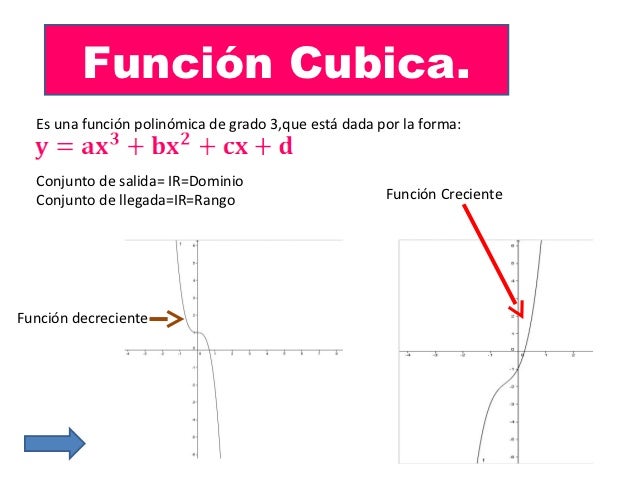
CUBUCA
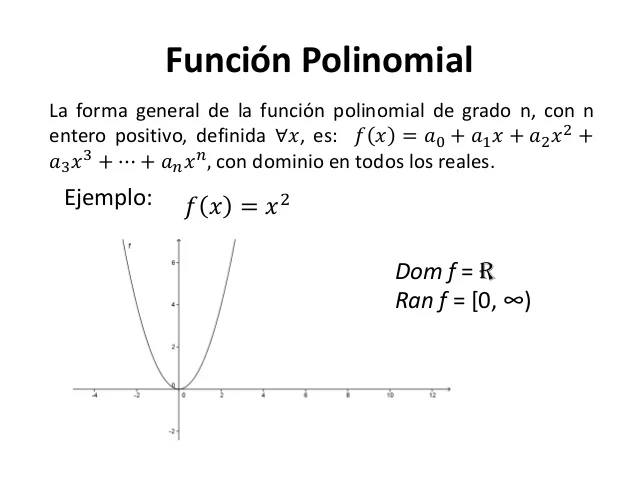
POLIMONIAL
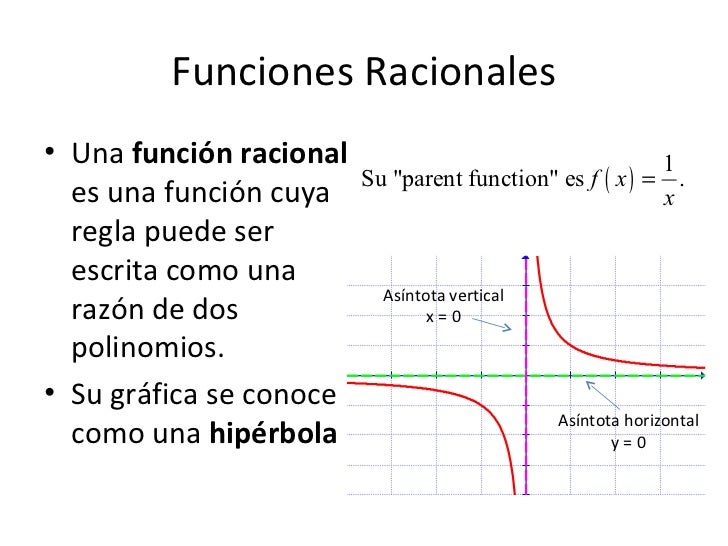
RACIONAL
IRRACIONAL
Una función racional f es una razón de dos polinomios, es decir, f (x)= p (x) / q (x)