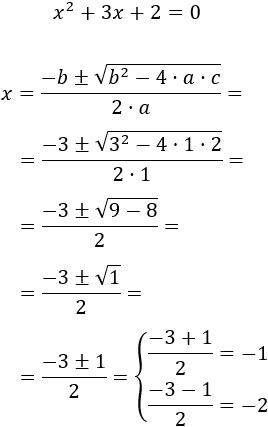Funciones polinomias de segundo grado y ecuaciones cuadraticas

Traslacion de una parabola

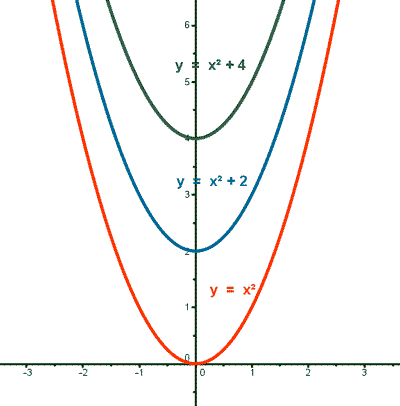
Traslacion vertical

y=x2+K
si k < 0 se desplaza hacia abajo
Si k > 0 se dezaplaza hacia arriba

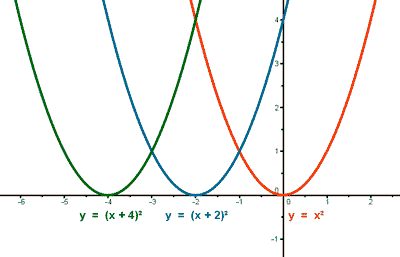
Traslacion Horizontal

y=(x+h)^2
Si h <0 se deszplaza hacia la izquierda de h
Si h>0 se deszaplaza hacia la derecha de h

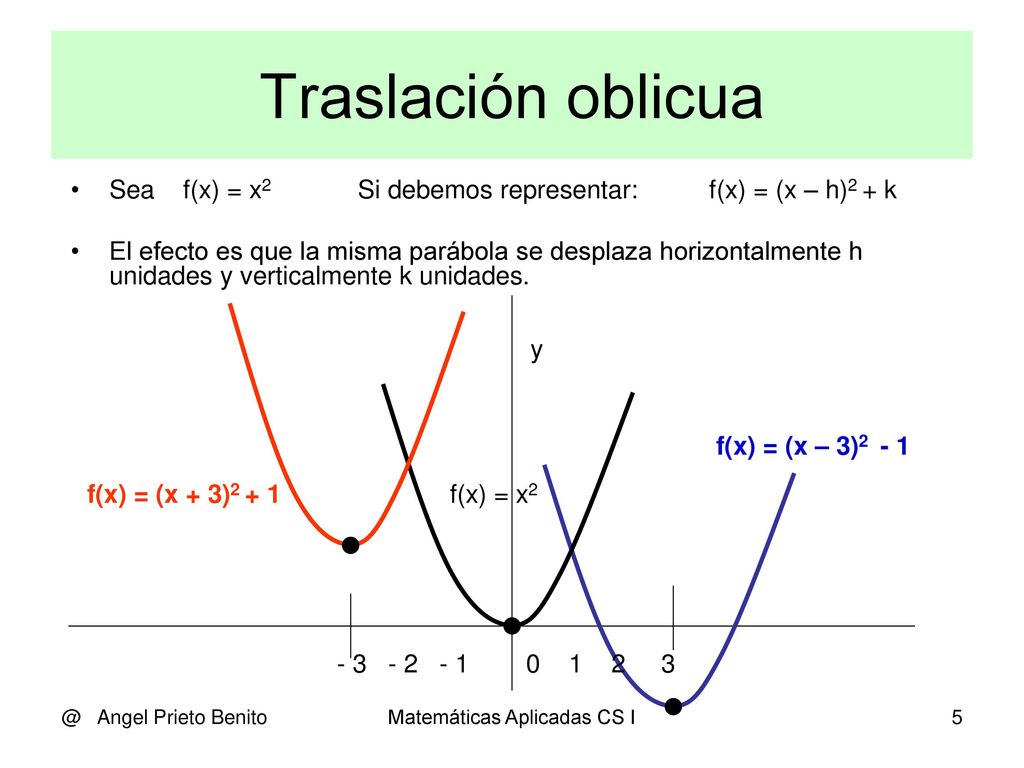
Traslacion oblicula

Y=(x+h)2+K

Ecuacion canonica

Es una manera de escrbir y describir
una parabola

Para analizar y sacar la formula canonica es

FP=√y^2+(x-p/2)^2
MP=p/2+x
FP=MP
√y^2+(x-p/2)^2=p/2+x
y^2+(x-p/2)^2=(p/2)^2+x^2+2.px/2

Se traduce a y^2=4px

Se puede sacar dos variables

Y=-√4px

y=+√4px

Como observamos la parabola se dirige a la derecha

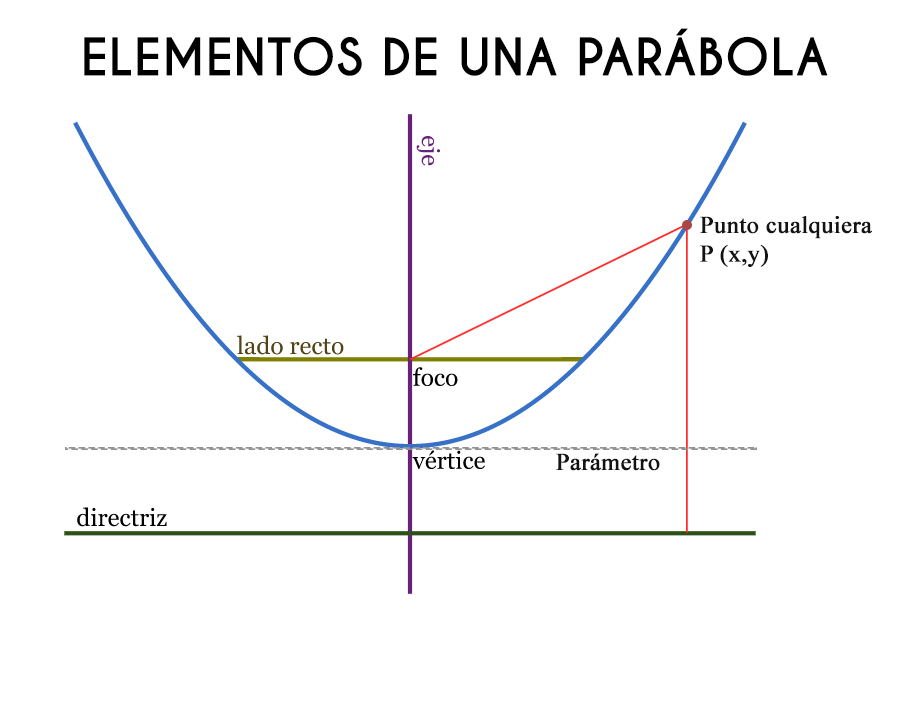
Eje de la parabola es el punto maximo

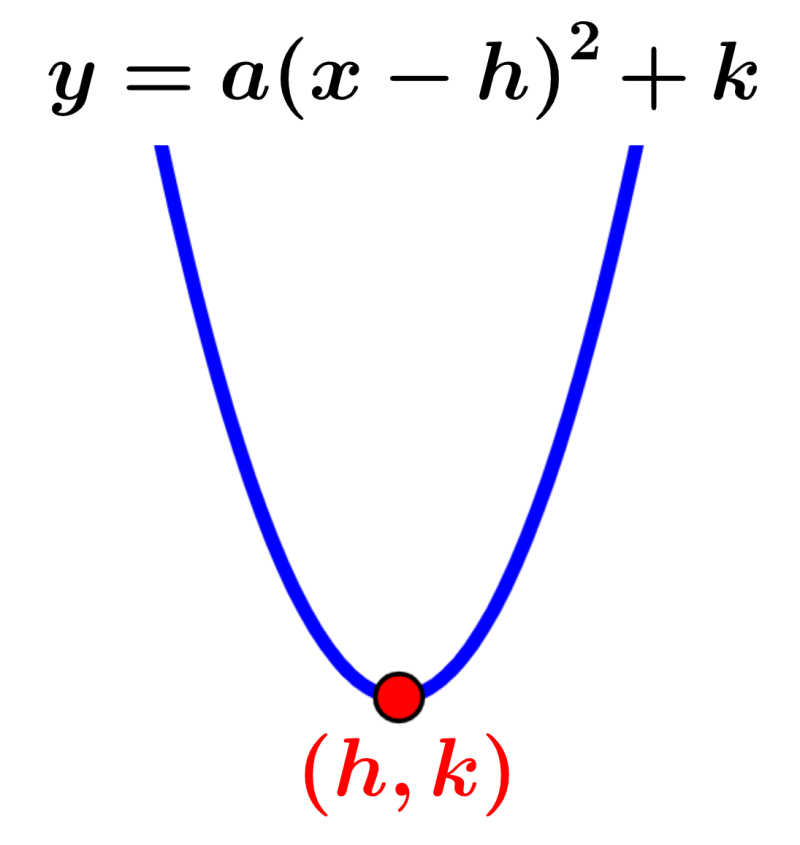
Vertice de la parabola (h,k)

Es el punto donde corta la
parabola en simetria

y=a(x–h)2+k

Foco

El foco es un punto fijo ubicado
en el interiro de la parabola

(h,k +1/(4a)).

Directriz

Son las lineas que representa
entre el foco y la directriz

Ejemplo de una parabola

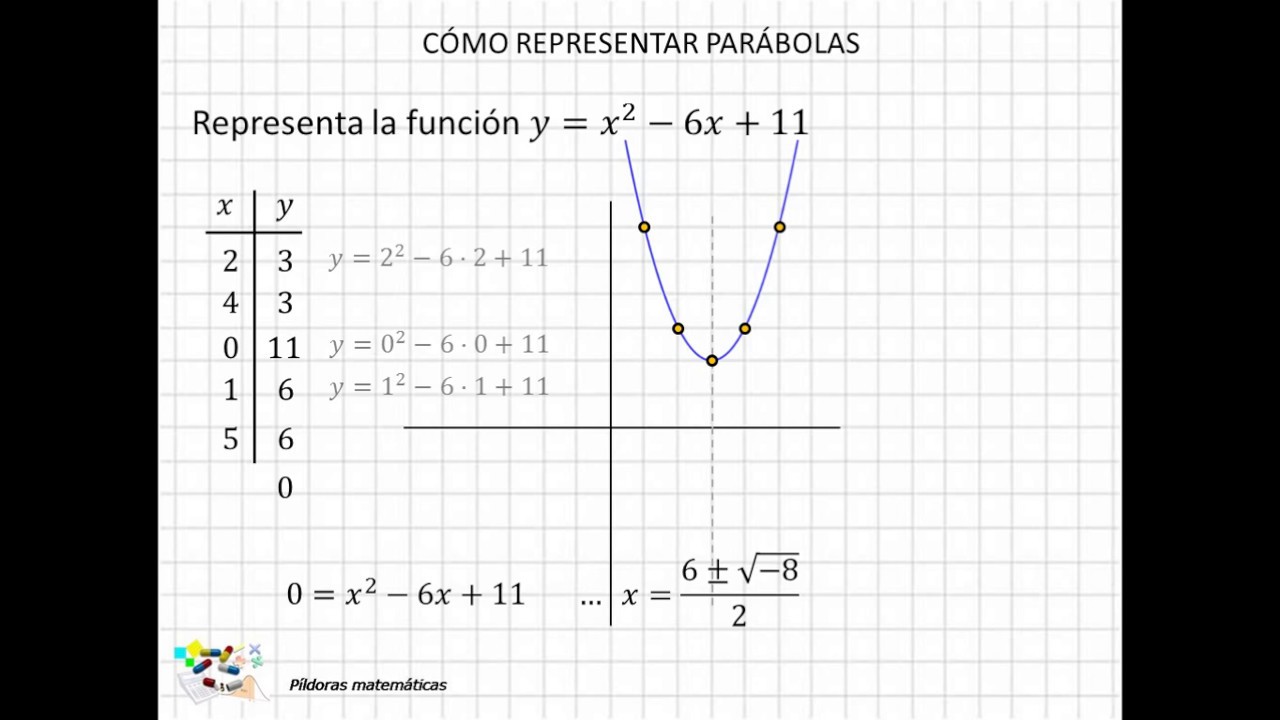
A es x2
B es -6x
C es el termino independiente que es 11

Si a es positivo la parabola va hacia arriba

Si a es negativo la parabola va hacia abajo

Se resuleve la ecuacion con la formula general
de ecuacioes de segundo grado

Son aquellas que tienen dos incognitas

Formulas de las ecuciones de
segundo grado

Ecuacion incompleta con b y c

x^2=0 la ecuacion es 0

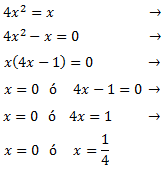
Ecuacion incompleta con c

ax^2+bx=0
factorizamos la ecuacion
ax^2 + bx = x(ax + b) = 0

Nos da dos posibles soluciones x=0
y x = -b/a

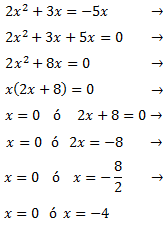
Ecuacion incompleta con B

ax^2 + c = 0

Da dos soluciones reales

x= √-c/a

x=-√-c/a

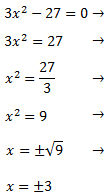
Ecuacion completa

Ax^2+Bx+C