Funciones T.9-10
Función
relación entre
X
Variable independiente
Y
Variable dependiente
Dominio y recorrido
Dominio
Dom f
variable independiente
Recorrido
Im f
variable dependiente
Continuidad y puntos de corte con los ejes
Continuidad
continua
puntos de discontinuidad
Subtema
Eje X
(a, 0); f(x) = 0
Eje Y
(0, b); f(0)
f(x1) < f(x2)
creciente
(a,b)
f(x1)> f(x2)
decreciente
(a,b)
f(x1) = f(x2)
constante
(a,b)
Máximo
x=a
en ese punto pasa de ser creciente a decreciente
Mínimo
x=a
en ese punto pasa de ser decreciente a creciente
Simetría y periodicidad
Simetrías
f(-x) = f(x)
función par
f(-x) = -f(x)
función impar
Periodicidad
f(x) = f(x+T) = f(x+ 2T) = ... = f(x+ k · T)
amplitud T del intervalo es el período con k un número entero
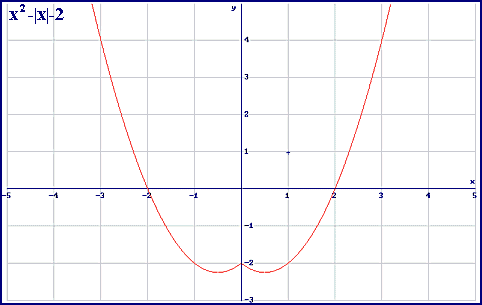
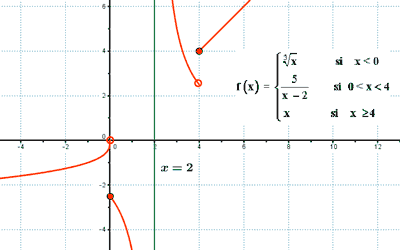
Funciones definidas a trozos
Funciones polinómicas de primer grado
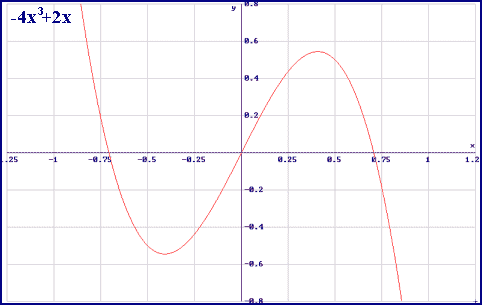
función polinómica
expresión algebraica es un polinomio
m = pendiente
n = ordenada en el origen
m > 0
crecientes
m < 0
decrecientes
m = 0
constantes
Tipos
y = ax² + bx + c; a≠0
gráfica
vértice
eje de simetría
a mayor valor absoluto de a, más cerradas estarán sus ramas
y = ax²
punto (0,0)
eje de simetría
Y
y = ax² + c
vértice
punto (0,0)
eje de simetría
Y
y = ax² + bx
forma oblicua la parábola y = ax²
vértice
punto de coordenadas
(-b/ 2a, -b²/ 4a)
eje de simetría
recta vertical de ecuación
x = -b/2a
y = ax² + b +c
vértice
( -b/ 2a, -b² + 4ac/ 4a)
eje de simetría
recta vertical x = -b/2a
a > 0
vértice es un mínimo de la función
a < 0
vértice es un máximo de la función