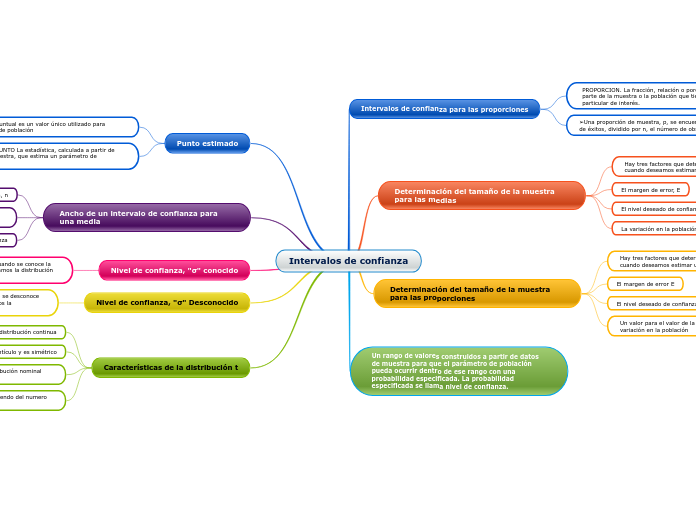
Intervalos de confianza
Intervalos de confianza para las proporciones
PROPORCION. La fracción, relación o porcentaje que indica la parte de la muestra o la población que tiene un rasgo particular de interés.
➢Una proporción de muestra, p, se encuentra por x, el número de éxitos, dividido por n, el número de observaciones
Determinación del tamaño de la muestra para las medias
Hay tres factores que determinan el tamaño de la muestra cuando deseamos estimar la media:
El margen de error, E
El nivel deseado de confianza, por ejemplo el 95%
La variación en la población
Determinación del tamaño de la muestra para las proporciones
Hay tres factores que determinan el tamaño de la muestra cuando deseamos estimar una proporción:
El margen de error E
El nivel deseado de confianza
Un valor para el valor de la palabra " π " para calcular la variación en la población
Un rango de valores construidos a partir de datos de muestra para que el parámetro de población pueda ocurrir dentro de ese rango con una probabilidad especificada. La probabilidad especificada se llama nivel de confianza.
Punto estimado
Una estimación puntual es un valor único utilizado para estimar un valor de población
ESTIMACIÓN DE PUNTO La estadística, calculada a partir de información de muestra, que estima un parámetro de población.
Ancho de un intervalo de confianza para una media
El número de observaciones en la muestra, n
La variabilidad en la población, generalmente estimada por la desviación estándar de la muestra, s
El nivel deseado de confianza
Nivel de confianza, "σ" conocido
Para determinar los límites de confianza cuando se conoce la desviación estándar de la población, utilizamos la distribución z
Nivel de confianza, "σ" Desconocido
Para determinar los límites de confianza cuando se desconoce la desviación estándar de la población, utilizamos la distribución t.
Características de la distribución t
La distribución t es una distribución continua
Tiene forma de montículo y es simétrico
Es mas plano, o mas extendido que la distribución nominal estándar
Hay una familia de distribuciones t, dependiendo del numero de grados de libertad