LA PARÁBOLA
Jennifer Ocampo
3ero BGU "B"
ELEMENTOS
Eje de Simetría.- Conocido también como "eje focal" se representa con la letra "l" y es la recta que divide a la parábola en 2 partes iguales, (el foco y el vértice son parte de esta recta).
Vértice.- Se representa con la letra "V" y es el punto de intersección entre la parábola y el eje de simetría.
Foco.- Se representa con la letra "F" y es el punto sobre el eje de simetría que está separado del vértice, por una distancia exactamente igual a la que separa el vértice de la directriz.
Directriz.- Se representa con la letra "d", es la recta perpendicular al eje de simetría tal que la distancia del vértice a la directriz es igual a la distancia del vértice al foco.
Lado Recto.- Se representa con las letras "LR", y es la cuerda perpendicular al eje de simetría y paralela a la directriz y que pasa por el foco. (Su longitud es 4 veces la distancia del vértice al foco).
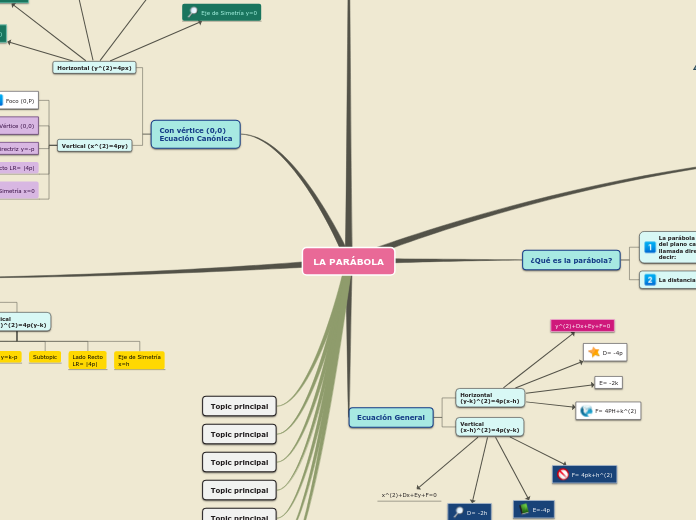
¿Qué es la parábola?
La parábola es el lugar geométrico de los punto P(x,y) del plano cartesiano que equidistan de una recta fija llamada directriz y de un punto fijo llamado foco, es decir:
La distancia desde (P,d)= d(P,f)
Ecuación General
Horizontal
(y-k)^(2)=4p(x-h)
F= 4PH+k^(2)
E= -2k
y^(2)+Dx+Ey+F=0
D= -4p
Vertical
(x-h)^(2)=4p(y-k)
D= -2h
E=-4p
F= 4pk+h^(2)
x^(2)+Dx+Ey+F=0
Con vértice (0,0)
Ecuación Canónica
Horizontal (y^(2)=4px)
Vértice (0,0)
Directriz x= -p
Lado Recto LR= |4p|
Foco (P,0)
Eje de Simetría y=0
Vertical (x^(2)=4py)
Foco (0,P)
Vértice (0,0)
Directriz y=-p
Lado Recto LR= |4p|
Eje de Simetría x=0
Con vértice (h,k)
Ecuación Canónica
Horizontal
(y-k)^(2)=4p(x-h)
Foco (h+p,k)
Vértice (h,k)
Directriz x=h-p
Lado Recto
LR= |4p|
Eje de Simetría
y=k
Vertical
(x-h)^(2)=4p(y-k)
Foco (h,k+p)
Vértice (h,k)
Directriz y=k-p
Subtopic
Lado Recto
LR= |4p|
Eje de Simetría
x=h