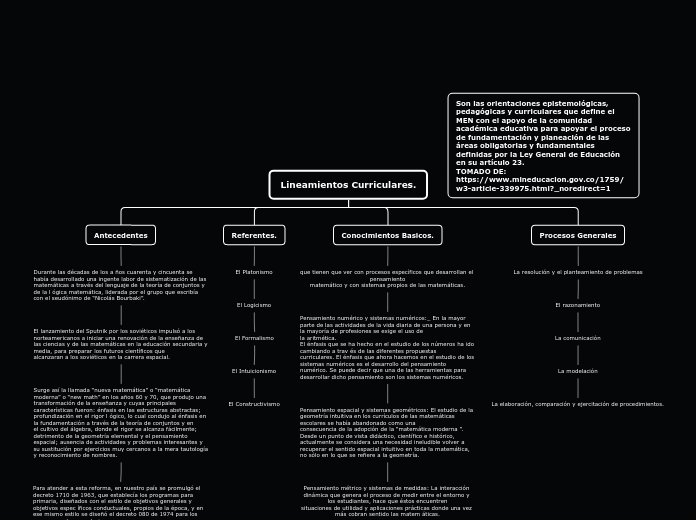
Lineamientos Curriculares.
Antecedentes
Durante las décadas de los a ños cuarenta y cincuenta se había desarrollado una ingente labor de sistematización de las
matemáticas a través del lenguaje de la teoría de conjuntos y de la l ógica matemática, liderada por el grupo que escribía
con el seudónimo de “Nicolás Bourbaki”.
El lanzamiento del Sputnik por los soviéticos impulsó a los norteamericanos a iniciar una renovación de la enseñanza de
las ciencias y de las matemáticas en la educación secundaria y media, para preparar los futuros científicos que
alcanzaran a los soviéticos en la carrera espacial.
Surge así la llamada “nueva matemática” o “matemática moderna” o “new math” en los años 60 y 70, que produjo una
transformación de la enseñanza y cuyas principales características fueron: énfasis en las estructuras abstractas;
profundización en el rigor l ógico, lo cual condujo al énfasis en la fundamentación a través de la teoría de conjuntos y en
el cultivo del álgebra, donde el rigor se alcanza fácilmente; detrimento de la geometría elemental y el pensamiento
espacial; ausencia de actividades y problemas interesantes y su sustitución por ejercicios muy cercanos a la mera tautología y reconocimiento de nombres.
Para atender a esta reforma, en nuestro país se promulgó el decreto 1710 de 1963, que establecía los programas para
primaria, diseñados con el estilo de objetivos generales y objetivos espec íficos conductuales, propios de la época, y en
ese mismo estilo se diseñó el decreto 080 de 1974 para los programas de secundaria.
Decreto 1710 de 1963,
Años 70
Años 70 y 80.
1975,
1978,
Ley General de Educación, Ley 115 de 1994
Referentes.
El Platonismo
El Logicismo
El Formalismo
El Intuicionismo
El Constructivismo
Conocimientos Basicos.
que tienen que ver con procesos específicos que desarrollan el pensamiento
matemático y con sistemas propios de las matemáticas.
Pensamiento numérico y sistemas numéricos:_ En la mayor parte de las actividades de la vida diaria de una persona y en la mayoría de profesiones se exige el uso de
la aritmética.
El énfasis que se ha hecho en el estudio de los números ha ido cambiando a trav és de las diferentes propuestas
curriculares. El énfasis que ahora hacemos en el estudio de los sistemas numéricos es el desarrollo del pensamiento
numérico. Se puede decir que una de las herramientas para desarrollar dicho pensamiento son los sistemas numéricos.
Pensamiento espacial y sistemas geométricos: El estudio de la geometría intuitiva en los currículos de las matemáticas escolares se había abandonado como una
consecuencia de la adopción de la “matemática moderna ”. Desde un punto de vista didáctico, científico e histórico,
actualmente se considera una necesidad ineludible volver a recuperar el sentido espacial intuitivo en toda la matemática,
no sólo en lo que se refiere a la geometría.
Pensamiento métrico y sistemas de medidas: La interacción dinámica que genera el proceso de medir entre el entorno y los estudiantes, hace que éstos encuentren
situaciones de utilidad y aplicaciones prácticas donde una vez más cobran sentido las matem áticas.
El pensamiento aleatorio y los sistemas de datos: Una tendencia actual en los currículos de matemáticas es la de favorecer el desarrollo del pensamiento aleatorio, el cual
ha estado presente a lo largo de este siglo, en la ciencia, en la cultura y aún en la forma de pensar cotidiana.
Pensamiento variacional y sistemas algebraicos y analíticos: Proponer el inicio y desarrollo del pensamiento variacional como uno de los logros para alcanzar en la educación básica,
presupone superar la enseñanza de contenidos matemáticos fragmentados y compartimentalizados, para ubicarse en el
dominio de un campo conceptual, que involucra conceptos y procedimientos interestructurados y vinculados que
permitan analizar, organizar y modelar matemáticamente situaciones y problemas tanto de la actividad práctica del
hombre, como de las ciencias y las propiamente matemáticas donde la variación se encuentre como sustrato de ellas.
Procesos Generales
La resolución y el planteamiento de problemas
El razonamiento
La comunicación
La modelación
La elaboración, comparación y ejercitación de procedimientos.