Números racionales ^
Definición
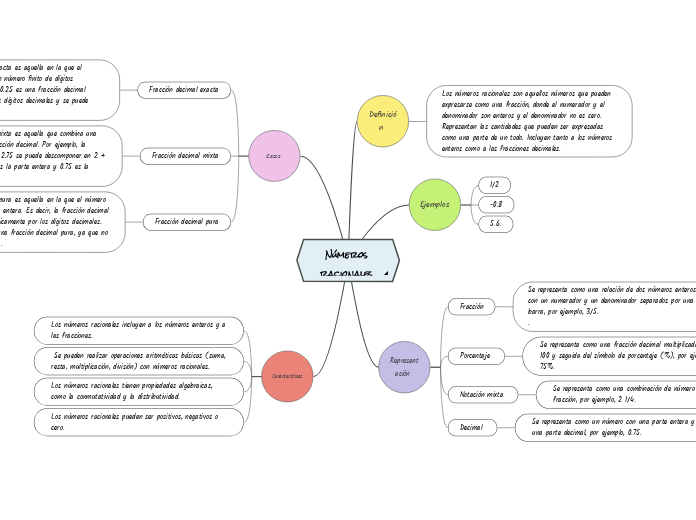
Los números racionales son aquellos números que pueden expresarse como una fracción, donde el numerador y el denominador son enteros y el denominador no es cero. Representan las cantidades que pueden ser expresadas como una parte de un todo. Incluyen tanto a los números enteros como a las fracciones decimales.
Ejemplos
1/2
-0.8
5.6.
Representación
Fracción
Se representa como una relación de dos números enteros, con un numerador y un denominador separados por una barra, por ejemplo, 3/5.
.
Porcentaje
Se representa como una fracción decimal multiplicada por 100 y seguida del símbolo de porcentaje (%), por ejemplo, 75%.
Notación mixta
Se representa como una combinación de número entero y fracción, por ejemplo, 2 1/4.
Decimal
Se representa como un número con una parte entera y una parte decimal, por ejemplo, 0.75.
Casos
Fracción decimal exacta
Una fracción decimal exacta es aquella en la que el número decimal tiene un número finito de dígitos decimales. Por ejemplo, 0.25 es una fracción decimal exacta, ya que tiene dos dígitos decimales y se puede representar como 1/4.
Fracción decimal mixta
Una fracción decimal mixta es aquella que combina una parte entera y una fracción decimal. Por ejemplo, la fracción decimal mixta 2.75 se puede descomponer en 2 + 0.75. En este caso, 2 es la parte entera y 0.75 es la fracción decimal.
Fracción decimal pura
Una fracción decimal pura es aquella en la que el número decimal no tiene parte entera. Es decir, la fracción decimal pura se representa únicamente por los dígitos decimales. Por ejemplo, 0.75 es una fracción decimal pura, ya que no tiene una parte entera.
Características
Los números racionales incluyen a los números enteros y a las fracciones.
Se pueden realizar operaciones aritméticas básicas (suma, resta, multiplicación, división) con números racionales.
Los números racionales tienen propiedades algebraicas, como la conmutatividad y la distributividad.
Los números racionales pueden ser positivos, negativos o cero.