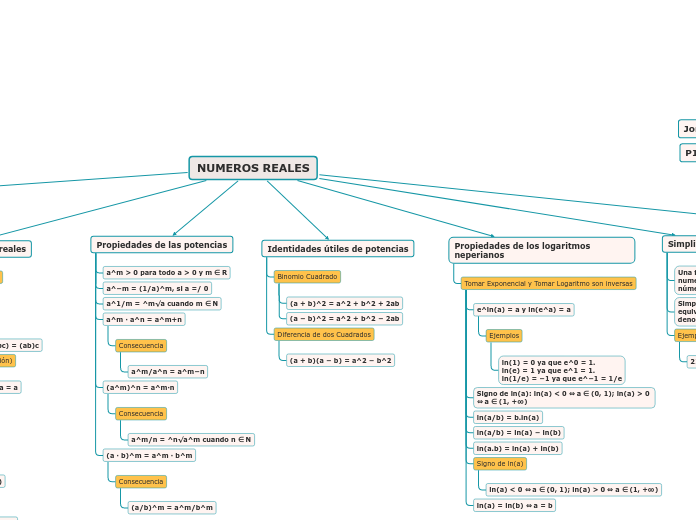
NUMEROS REALES
Definición
Conjunto de los números naturales
N= {1, 2, 3, . . .}
Conjunto de los números enteros
Z= {0, ±1, ±2, ±3, . . .}
Conjunto de los números racionales:
Q={a/b , a, b ∈ Z, b =/ 0}
Conjunto de los números irracionales
a/b , a, b ∈ Z, b =/ 0
Conjunto de los números reales
R es la unión de los números
racionales e irracionales
Valor absoluto de un n´umero real a que se denota como |a| es
|a| ={ a si x ≥ 0}
{−a si x < 0}
Potencia de base (a) y exponente (m)
Se denota por am la potencia de base a y exponente m, con a y m ∈ R
Logaritmo neperiano del número (a)
ln(a) = b ⇔ e^b = a
Fracciones equivalentes
a/b y c/d son equivalentes si y s´olo si a.d = b.c
Fracción irreducible
a/b es una fracción irreducible si a y b son primos entre sí
Propiedades de los números reales
Conmutativa (Suma y Multiplicación)
a + b = b + a | ab = ba
Asociativa (Suma y Multiplicación)
a + (b + c) = (a + b) + c | a(bc) = (ab)c
Elemento neutro (Suma y Multiplicación)
a + 0 = 0 + a = a | a · 1 = 1 · a = a
Elemento opuesto (Suma)
a + (−a) = (−a) + a = 0
Consecuencia (Resta)
a − b significa a + (−b)
Elemento inverso (Multiplicación)
para a =/ 0, a · a−1 = a−1 · a = 1
Consecuencia (División)
a/b significa a · b^−1.
Distributiva (multiplicación) respecto (Suma)
a(b + c) = a · b + a · c.
Propiedades de las potencias
a^m > 0 para todo a > 0 y m ∈ R
a^−m = (1/a)^m, si a =/ 0
a^1/m = ^m√a cuando m ∈ N
a^m · a^n = a^m+n
Consecuencia
a^m/a^n = a^m−n
(a^m)^n = a^m·n
Consecuencia
a^m/n = ^n√a^m cuando n ∈ N
(a · b)^m = a^m · b^m
Consecuencia
(a/b)^m = a^m/b^m
Identidades útiles de potencias
Binomio Cuadrado
(a + b)^2 = a^2 + b^2 + 2ab
(a − b)^2 = a^2 + b^2 − 2ab
Diferencia de dos Cuadrados
(a + b)(a − b) = a^2 − b^2
Propiedades de los logaritmos neperianos
Tomar Exponencial y Tomar Logaritmo son inversas
e^ln(a) = a y ln(e^a) = a
Ejemplos
ln(1) = 0 ya que e^0 = 1.
ln(e) = 1 ya que e^1 = 1.
ln(1/e) = −1 ya que e^−1 = 1/e
Signo de ln(a): ln(a) < 0 ⇔ a ∈ (0, 1); ln(a) > 0 ⇔ a ∈ (1, +∞)
ln(a/b) = b.ln(a)
ln(a/b) = ln(a) − ln(b)
ln(a.b) = ln(a) + ln(b)
Signo de ln(a)
ln(a) < 0 ⇔ a ∈ (0, 1); ln(a) > 0 ⇔ a ∈ (1, +∞)
ln(a) = ln(b) ⇔ a = b
Operaciones con fracciones
Suma de fracciones
Para sumar dos fracciones con el mismo denominador se suman los numeradores y se deja el denominador común
Para sumar dos fracciones con distinto denominador, primero se reducen a común denominador y después se efectúa la suma
a/b + c/b = a + c/b
División de fracciones
Para dividir dos fracciones se multiplica la primera
por la inversa de la segunda.
Fracción inversa
La fracción inversa de a/b es b/a
Multiplicación de fracciones
El producto de dos fracciones es una nueva
fracción que tiene por denominador el producto de los numeradores y por denominador el producto de los denominadores de las fracciones que se multiplican
a/b . c/d = a . c/b . d
Simplificación de fracciones
Una forma de simplificar una fracción es dividir numerador y denominador por el mismo número
Simplificar una fracción es obtener otra equivalente a ella que tenga en el numerador y denominador números más pequeños
Ejemplo
21/28 = 3 · 7/2^2 · 7 = 3/2^2 = 3/4