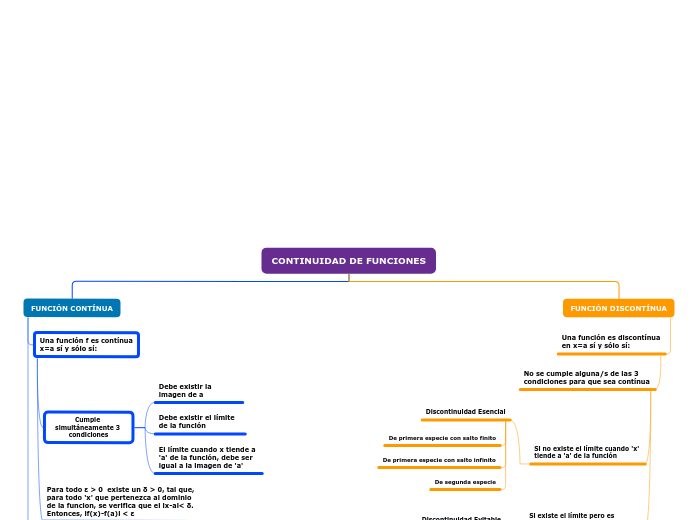
CONTINUIDAD DE FUNCIONES

Debe existir la imagen de a

Debe existir el límite de la función

El límite cuando x tiende a 'a' de la función, debe ser igual a la imagen de 'a'

Para todo ε > 0 existe un δ > 0, tal que, para todo 'x' que pertenezca al dominio de la funcion, se verifica que el lx-al< δ. Entonces, lf(x)-f(a)l < ε

En un intervalo

Límites laterales (por izquierda y por derecha)

f es contínua a DERECHA sí y sólo sí el límite cuando 'x' tiende a x0 de la función es igual a la imagen de x0

f es contínua a IZQUIERDA en x=x0 si y sólo si el límite cuando 'x' tiende a x0 de la función es igual a la imagen de x0

Abierto

(a;b)

f es contínua en (a;b) sí y sólo sí f es contínua en todos los puntos interiores del intervalo

Para todo 'c' que pertenece al intervalo, el limite cuando 'x' tiende a 'c' de la funcion, es igual a la imagen de 'c'

Cerrado

[a;b]

f es contínua en [a;b] sí y sólo sí f es contínua en (a;b), es contínua a derecha en x=a y es contínua a izquierda en x=b

Para todo 'c' que pertenece a (a;b) se verifica que el limite cuando 'x' tiende a 'c' de la función es igual a la imagen de 'c' y el límite cuando 'x' tiende a 'a' tanto por izquierda como por derecha de la funcion son iguales a la imagen de 'b'

Una función es discontínua en x=a sí y sólo sí:

No se cumple alguna/s de las 3 condiciones para que sea contínua

Si no existe el límite cuando 'x' tiende a 'a' de la función

Discontinuidad Esencial

De primera especie con salto finito

De primera especie con salto infinito

De segunda especie

Si existe el límite pero es distinto de la imagen de 'a'

Discontinuidad Evitable