RAPPRESENTAZIONI NUMERICHE NEL COMPUTER
CONVERSIONI
Nella conversione, il processo che ci permette di convertire un numero in un’altra base qualsiasi, l’ultima cifra da destra equivale alle unità, la seconda alle decine e così via.

da base b a base 10
Per svolgere una conversione da base 2 a base 10 si usa la forma polinomia, cioè la sommatoria di ciascuna cifra moltiplicata per la base elevata alla sua posizione.Ad esempio:(1011)₂=1x2º+1x2¹+0x2²+1x2³=(11)₁₀

da base 10 a base b
Per convertire invece, da base 10 a base 2, si utilizza il metodo delle divisioni successive:(137)₁₀= (10001001)₂ Per scrivere il risultato, si inizia a leggere da sotto e si scrivono le cifre da sinistra a destra.

con le tabelle
Per convertire un numero in base 2 in uno in base 8 o 16 utilizzeremmo delle conversioni indirette, cioè passare dalla base 2 alla base 10 per poi arrivare alle base 8 o 16. C’è però un metodo più veloce, utilizzare le conversioni con le tabelle. Questo metodo si serve di due tabelle, quella per la base 8 e quella per la base 16:La tabella per la base 8 si costruisce scrivendo le cifre da 0 a 7 in verticale e, partendo dall’ultima colonna a destra, alternare l’1 allo 0, raddoppiando le cifre andando verso la colonna sinistra.La tabella per la base 16, invece, si costruisce scrivendo le cifre da 0 a 9 e le lettere da A a F in verticale, e usando poi lo stesso procedimento usato per la tabella precedente.Esempio di conversione in base 8:(100110)₂=(46)₈ perchè 110=6e 100=4.Esempio di conversione in base 16:(1101110110)₂=(376)₁₆perchè 0110=6,0111=7e 0011=3. (le cifre in rosso sono aggiunte in modo da poter fare la conversione, quindi arrivare a 4 cifre).Abbiamo quindi preso tre cifre partendo da sinistra per la base 8 e quattro per la base 16.
RAPPRESENTAZIONI PER NUMERI RELATIVI
MODULO E SEGNO
La rappresentazione in modulo e segno si svolge partendo dalla conversione: in questo caso -90 diventa (1011010) in binario.Essendo però un numero negativo e dovendo raggiungere 8 bit, la rappresentazione finale in modulo e segno di -90 diventa: 11011010. La cifra in rosso rappresenta il meno, infatti questo segno viene rappresentato appunto con l’1, mentre il + con lo 0.
COMPLEMENTO A 2
La rappresentazione in complemento a 2, invece, rimane invariata se dobbiamo convertire un numero positivo, quindi rimarrebbe la stessa usando il MS, mentre se bisogna rappresentare un numero negativo il discorso diventa un po’ più articolato; prendiamo ad esempio -102, facciamo la conversione in binario e troviamo (1100110). Adesso la conversione in MS del numero positivo sarebbe 01100110: queste cifre vanno adesso invertite, trovando il numero in complemento a uno, quindi 10011001. Questo numero va adesso sommato a 1, trovando quindi 10011010. La trasformazione in complemento a due è completata.
SISTEMI DI NUMERAZIONE
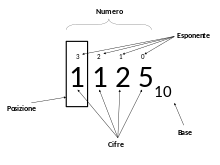
posizionali
I sistemi posizionali sono: il sistema decimale, ottale, binario, esadecimale,ecc.
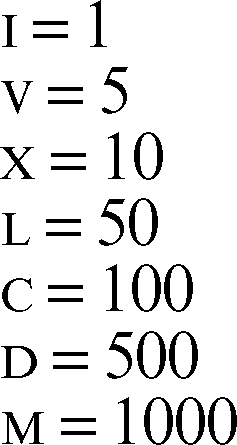
non posizionali
Il sistema non posizionale principale è quello dei numeri romani.
RAPPRESENTAZIONI PER NUMERI REALI
Le due rappresentazioni possibili per i numeri reali sono in VIRGOLA FISSA(fixed point) e in VIRGOLA MOBILE(floating point).

VIRGOLA FISSA
La rappresentazione in virgola fissa richiede un formato di 16 bit: 1 per il segno, 7 per la parte intera e 8 per la parte decimale. Partendo dal numero -36,625, svolgiamo la conversione in binario della parte intera, ottenendo (100100) e in seguito, utilizzando il metodo delle moltiplicazioni successive, moltiplichiamo la parte decimale fino a trovare un numero intero:0,625x 2 = Le cifre in rosso vengono tolte dalla moltiplicazione e messe nella rappresentazione finale1,25020,50021,000La rappresentazione finale è quindi:1010010010100000Con il primo 1 che indica il segno, le successive 7 cifre la parte intera(lo 0 in rosso per completare i 7 bit) e le altre 8 per la parte decimale(gli ultimi 5 zeri in rosso per completare gli 8 bit).

VIRGOLA MOBILE
Passiamo invece alla conversione in virgola mobile che si serve di 32 bit.Partiamo dal numero +43,6875. Come sempre facciamo la conversione della parte intera, ottenendo 101011, e della parte decimale:0,6875x21,3750 Anche in questo le cifre intere vanno poi usate nella rappresentazione finale.20,75021,50023,000Mettendo quindi insieme la parte intera e quella decimale, otteniamo 101011,1011.A questo punto dobbiamo NORMALIZZARE, cioè portare la virgola fino alla prima cifra a sinistra, quindi 1,010111011x2⁵(alla quinta perchè abbiamo spostato la virgola di 5 posizioni).Le cifre dopo la virgola fanno parte della MANTISSA. Ora dobbiamo POLARIZZARE: il 5 viene sommato a 127(BIAS),ottenendo 132. Questo numero viene convertito in binario, ottenendo 10000100, che forma l’ESPONENTE.Possiamo quindi procedere a rappresentare in virgola mobile:010000100010111011000000000000000con lo 0 in blu che indica il segno, la parte in verde che indica l’esponente, la parte in giallo che indica la prima parte della mantissa e i restanti 0 in rosso che completano la mantissa.
