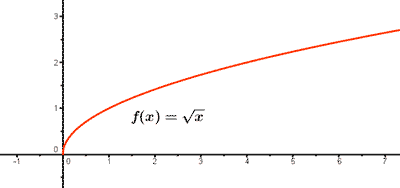Funciones Algebraicas
Funciones Exponenciales
Características
Dominio: Dominio de la función exponencial.
El dominio son todos los números reales.
Recorrido: Recorrido de la función exponencial.
El recorrido son todos los números reales positivos.
Derivada de la función exponencial: Derivada de la función exponencial.
Concepto: Una función exponencial es aquella que la variable independiente x aparece en el exponente y tiene de base una constante a. Su expresión es:
Expresión general de una función exponencial.
siendo a un real positivo, a > 0, y diferente de 1, a ≠ 1.

La función exponencial puede considerarse como la inversa de la función logarítmica.

Ejemplo
Función logarítmica
Concepto:
Una función logarítmica está formada por un logaritmo de base a, y es de la forma:
Expresión general de una función logarítmica.
siendo a un real positivo, a > 0, y diferente de 1, a ≠ 1.


Ejemplo
Características
Dominio: Dominio de la función logarítmica.
El dominio son todos los números reales positivos.
Recorrido: Recorrido de la función logarítmica.
El recorrido son todos los números reales.
Derivada de la función logarítmica: Derivada de la función logarítmica.
Las funciones logarítmicas son continuas.
Si a es mayor que 1 (a > 1), la función es estrictamente creciente. En cambio, si a es menor que 1 (a < 1), la función es estrictamente decreciente.
Funciones Polinómicas
Concepto:
Una función polinómica f es una función cuya expresión es un polinomio tal como:
El dominio de las funciones polinómicas son todos los números reales.
Las funciones polinómicas son continuas en todo su dominio.

Propiedades de las funciones polinómicas
Sean f(x) y g(x) dos funciones polinómicas, entonces:
La suma de dos funciones polinómicas es una función polinómica. Es decir:
f(x)+g(x) es polinómica

Ejemplo
Función racional

Concepto: Una función racional f(x) es el cociente de dos polinomios. La palabra racional hace referencia a que esta función es una razón.
P(x) es el polinomio del numerador y Q(x) el del denominador.
El dominio de una función racional son todos los números reales los valores de la variable x que anulan el denominador (Q(x)) = 0), es decir, excepto las raíces del polinomio correspondiente.

Ejemplo:
Función Irracional
Concepto: Las funciones con radicales son las funciones que tienen la variable independiente x bajo el signo radical, es decir:
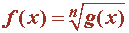
Las características generales de las funciones con radicales son:
1) Si n es un número par su dominio es el intervalo en el que g(x) ≥ 0 .
2) Si n es impar, su dominio es R.
3) Su representación gráfica es una rama de una parábola.
Ejemplo:
1) Ejemplo de función irracional: f(x) = √x
1) Dominio:
Como n es par, el dominio de f(x) es el conjunto de valores donde x ≥ 0 , es decir, Dom(f) = [0, +∞)
2) Puntos de corte:
f(0) = √0 = 0 , es decir, el punto de corte coincide con el eje de coordenadas (0, 0).