SISTEMAS DE NUMERACIÓN
LOS SÍMBOLOS
Cada sistema de numeración tiene un número limitado de símbolos que coincide con la base del sistema
SISTEMA BINARIO
BASE 2
SÍMBOLOS 0 y 1
En los ordenadores los datos se almacenan en binario
SISTEMA OCTAL
BASE 8
SÍMBOLOS 0, 1, 2, 3, 4, 5, 6 y 7
Para manejo de números muy grandes
SISTEMA DECIMAL
BASE 10
SÍMBOLOS 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9
Sistema de numeración más habitual en el hombre
Añadir texto
SISTEMA HEXADECIMAL
BASE 16
SÍMBOLOS 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E y F
Para manejo de números muy grandes
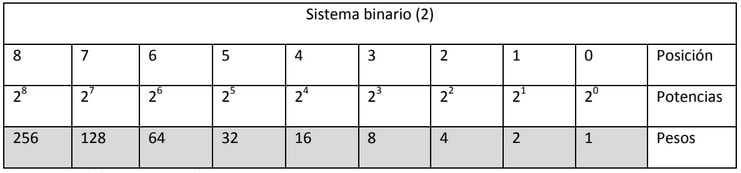
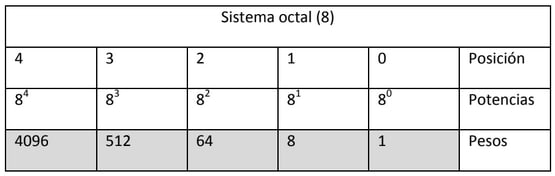
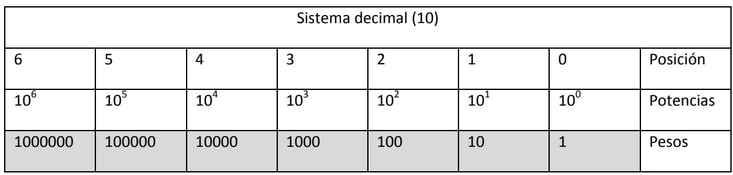
LOS PESOS
Cada símbolo del sistema representa un valor o peso en función de la posición que ocupe en el número
Tablas de pesos según el sistema de numeración
Añadir texto
Añadir texto
Añadir texto

Añadir texto
CONVERSIÓN
DEL DECIMAL AL RESTO: POR RESTOS
AL BINARIO
Dividimos consecutivamente por 2, obteniendo como restos 0
y 1
AL OCTAL
Dividimos consecutivamente por 8, obteniendo como restos
símbolos menores que 8 (0..7)
Una vez obtenidos todos los restos han de colocarse en el orden correcto, es decir, se toman todos los restos, de abajo a arriba, y se ordenan de izquierda a derecha.
AL HEXADECIMAL
Dividimos consecutivamente por 16, obteniendo como
restos números menores que 16 (0..15)
DEL DECIMAL AL BINARIO: POR PESOS

Para representar un valor decimal en binario hay que desglosarlo en estos pesos. Al final, los pesos elegidos han de sumar el número decimal. Para hacerlo, ha de asignarle el mayor peso que “quepa”, y a continuación repetir la operación con lo que quede hasta completar la suma.undefined
CONVERSIÓN ENTRE BINARIO, OCTAL Y HEXADECIMAL: POR GRUPOS
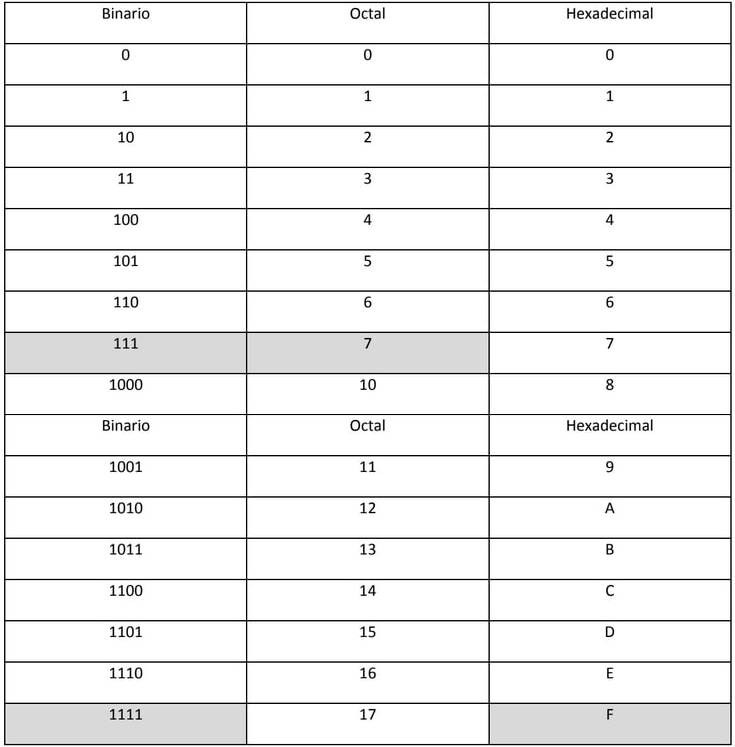
Estos tres sistemas tienen en común que su base (2^0, 2^3, 2^4) es múltiplo de dos. A continuación se muestra la tabla de correspondencia entre los tres sistemas.
OPERACIONES BOOLEANAS
1.
El Álgebra de Bool es una parte de las Matemáticas dedicada a las operaciones lógicas.
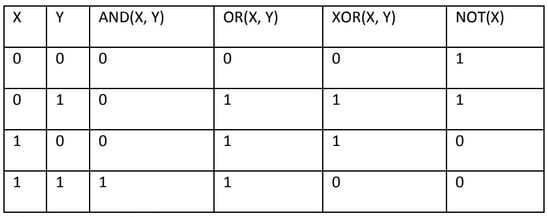
- Para conseguir el resultado 1 (verdad) con el operador AND, todos los operadores han de ser 1 (verdad). Han de ser verdad uno Y otro. En cualquier otro caso, el resultado es 0 (falso).
- Para conseguir el resultado 1 (verdad) con el operador OR, ha de aparecer un 1 (verdad) en alguno de los operadores. Han de ser verdad uno u(O) otro. Sólo si todos los operadores son 0 (falso) el resultado es 0 (falso).
- Para conseguir el resultado 1 (verdad) con el operador XOR, ha de aparecer sólo un 1 (verdad) en alguno de los operadores. Han de ser verdad uno u(O) otro de forma EXCLUSIVA. En cualquier otro caso, el resultado es 0 (falso).
- El operador NOT niega (cambia) el valor del operando.