Teoria de grafos

arbol
Un árbol es un grafo conexo simple acíclico. Algunas veces, un vértice del árbol es distinguido llamándolo raíz. Los árboles se usan frecuentemente como estructuras de datos en ciencias de la computación (véase árbol).

Camino/ciclo hamiltoniano
Camino hamiltoniano
Existe un concepto dual al de camino/ciclo Euleriano. Un camino hamiltoniano en un grafo es un camino que "visita" cada vértice una y sólo una vez

Un ciclo euleriano en un grafo es un ciclo que usa cada arista una y sólo una vez.

Un Ciclo (o circuito) es un camino que empieza y acaba en el mismo vértice. Los ciclos de longitud 1 se denominan lazos o bucles.
Un ciclo simple es un ciclo que tiene como longitud al menos 3 y en el que el vértice inicial coincide con el vértice final.

En Teoría de Grafos, se llama Camino a una secuencia de vértices dentro de un grafo tal que exista una arista entre cada vértice y el siguiente. Se dice que dos vértices están conectados si existe un camino que vaya de uno a otro, de lo contrario estarán desconectados.

En Teoría de grafos, el grado o valencia de un vértice es el número de aristas incidentes al vértice. El grado de un vértice x es denotado por grado(x), g(x) o gr(x) (aunque también se usa δ(x), y del inglés d(x) y deg(x)). El grado máximo de un grafo G es denotado por Δ(G) y el grado mínimo de un grafo G es denotado por δ(G).

tra forma de definir el grado de un vértice es a través de su vecindad. La vecindad de un vértice x , denotado como N(x) está dado por todos los vértices adyacentes a x.
de modo que el grado del vértice x es el número de vecinos que tiene:
g(x) =|N(x)|

matriz de incidencia
La matriz de incidencia es una matriz binaria (sus elementos sólo pueden ser unos o ceros) que se utiliza como una forma de representar relaciones binarias.
Las columnas de la matriz representan las aristas del grafo.
Las filas representan a los distintos nodos.
Por cada nodo unido por una arista, ponemos un uno (1) en el lugar correspondiente, y llenamos el resto de las ubicaciones con ceros (0).

matriz de adyasencia
La matriz de adyacencia es una matriz cuadrada que se utiliza como una forma de representar relaciones binarias.

Subtema

Para un grafo no dirigido la matriz de adyacencia es simétrica.
El número de caminos Ci,j(k), atravesando k aristas desde el nodo i al nodo j, viene dado por un elemento de la potencia k-ésima de la matriz de adyacencia:

bucle
En teoría de grafos, un bucle o loop es una arista que conecta un vértice consigo mismo. Un grafo simple no posee bucles.

VERTICES ADYACENTES
En un grafo, dos vértices son adyacentes si están conectados por una arista

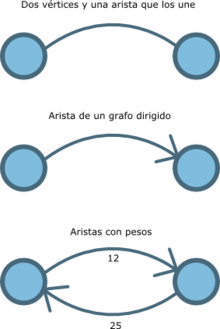
Un grafo dirigido o digrafo es un tipo de grafo en el cual las aristas tienen un sentido definido,1 a diferencia del grafo no dirigido, en el cual las aristas son relaciones simétricas y no apuntan en ningún sentido.

Un multigrafo o pseudografo es un grafo que está facultado para tener aristas múltiples; es decir, aristas que relacionan los mismos nodos. De esta forma, dos nodos pueden estar conectados por más de una arista. Formalmente, un multigrafo G es un par G:=(V, E) donde:
V es un conjunto de vértices o nodos
E es un multiconjunto de pares no ordenados de nodos, llamados aristas o líneas.

Grafo simple:
O simplemente grafo es aquel que acepta una sola arista uniendo dos vértices cualesquiera. Esto es equivalente a decir que una arista cualquiera es la única que une dos vértices específicos. Es la definición estándar de un grafo.
relacion binaria
en matematicas una relacion matematica R definida entre los elementos de dos conjuntos AyB.
una relacion R de A en B se puede representar mediante pares ordenados (a,b) para los cuales se cumple la propiedad P(a,b) de forma que (A,b) pertenece AXB

arbol de expansion
En teoría de grafos, un árbol de expansión, árbol generador o árbol recubridor T de un grafo conexo, no dirigido G es un árbol compuesto por todos los vértices y algunas (quizá todas) de las aristas de G. Informalmente, un árbol de expansión de G es una selección de aristas de G que forman un árbol que cubre todos los vértices. Esto es, cada vértice está en el árbol, pero no hay ciclos. Por otro lado, todos los puentes de G deben estar contenidos en T.

grafo (grafaica)
Es una estructura discreta que consiste de vértices (representados por puntos) y aristas (segmentos de recta que unen dos vértices).

punto (nodo)
es cualquier punto terminal de un segmneto