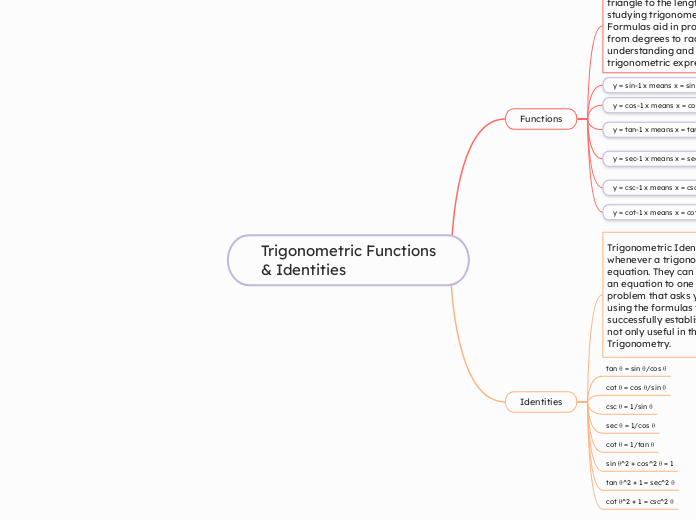
Trigonometric Functions & Identities
Functions
y = sin-1 x means x = sin y
Restrictions: -1 ≤ x ≤ 1, -3.14/2 ≤ y ≤ 3.14/2
y = cos-1 x means x = cos y
Restrictions: -1 ≤ x ≤ 1, 0 ≤ y ≤ 3.14
y = tan-1 x means x = tan y
Restrictions: - infinity ≤ x ≤ infinity, -3.14/2 ≤ y ≤ 3.14/2
y = sec-1 x means x = sec y
Restrictions: |x| ≥ 1, 0 ≤ y ≤ 3.14, y cannot equal 3.14/2
y = csc-1 x means x = csc y
Restrictions: |x| ≥ 1, -3.14/2 ≤ y ≤ 3.14, y cannot equal 0
y = cot-1 x means x = cot y
Restrictions: - infinity ≤ x ≤ infinity, 0 ≤ y ≤ 3.14
Identities
tan θ = sin θ/cos θ
cot θ = cos θ/sin θ
csc θ = 1/sin θ
sec θ = 1/cos θ
cot θ = 1/tan θ
sin θ^2 + cos^2 θ = 1
tan θ^2 + 1 = sec^2 θ
cot θ^2 + 1 = csc^2 θ