Precios Iniciar sesión Registrarse

Categorías: Todo - exponentes - reglas - fracciones - multiplicación

por daniela guzman hace 10 años

219

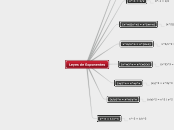
Leyes de Exponentes

Las leyes de exponentes son fundamentales para simplificar y resolver expresiones algebraicas que involucran potencias. Estas leyes incluyen la definición de exponentes negativos, que transforman una base elevada a un exponente negativo en una fracción, y la regla de cualquier número elevado a la potencia de cero, que siempre resulta en uno.

Los grandes imperios coloniales (3)-la administración colonial y sus efectos (4)

por María Úcar

Los numeros racionales

por Juan Diego Roman

PROPIEDADES DE LA MULTIPLICACIÓN

por SONIA YANETH FAJARDO OROZCO

Modelo Relacional

por Miguel Gallo

Leyes de Exponentes

x^-n = 1/x^n

Leyes de Exponentes

Los grandes imperios coloniales (3)-la administración colonial y sus efectos (4)

Los numeros racionales

PROPIEDADES DE LA MULTIPLICACIÓN

Modelo Relacional

Leyes de Exponentes

x^-n = 1/x^n

x^-3 = 1/x^3

(x/y)^n = x^n/y^n

(x/y)^2 = x^2 / y^2

(xy)^n = x^ny^n

(xy)^3 = x^3y^3

(x^m)^n = x^(m)(n)

(x^2)^3 = x^(2)(3) = x^6

x^m/x^n = x^(m-n)

x^4/x^2 = x^(4-2) = x^2

(x^m)(x^n) = x^(m+n)

(x^2)(x^3) = x^(2+3) = x^5

x^-1 = 1/x

4^-1 = 1/4

x^0 = 1

7^0 = 1

x^1 = x

6^1 = 6

Mindomo

Más información

Preguntas Frecuentes

Leyes de Exponentes

Los grandes imperios coloniales (3)-la administración colonial y sus efectos (4)

Los numeros racionales

PROPIEDADES DE LA MULTIPLICACIÓN

Modelo Relacional

Leyes de Exponentes

x^-n = 1/x^n

x^-3 = 1/x^3

(x/y)^n = x^n/y^n

(x/y)^2 = x^2 / y^2

(xy)^n = x^ny^n

(xy)^3 = x^3y^3

(x^m)^n = x^(m)(n)

(x^2)^3 = x^(2)(3) = x^6

x^m/x^n = x^(m-n)

x^4/x^2 = x^(4-2) = x^2

(x^m)(x^n) = x^(m+n)

(x^2)(x^3) = x^(2+3) = x^5

x^-1 = 1/x

4^-1 = 1/4

x^0 = 1

7^0 = 1

x^1 = x

6^1 = 6

Difunde Mindomo

Mindomo

Más información

Preguntas Frecuentes