Organigrama arbol

Ver más

Características de la administración.

por Yamile Martinez Mancillla

SISTEMA ACUSATORIO

por karen Sanchez

Funciones del Lenguaje Se entiende por las funciones del lenguaje a los distintos cometidos con que el ser humano emplea el lenguaje, es decir, los propósitos comunicativos con los que utiliza esa herramienta cognitiva y abstracta.

por DAYANA LIZBETH CAICEDO ESPINOSA

Sistema Nervioso Periferico

por Safira Cortes

CONTINUIDAD DE FUNCIONES

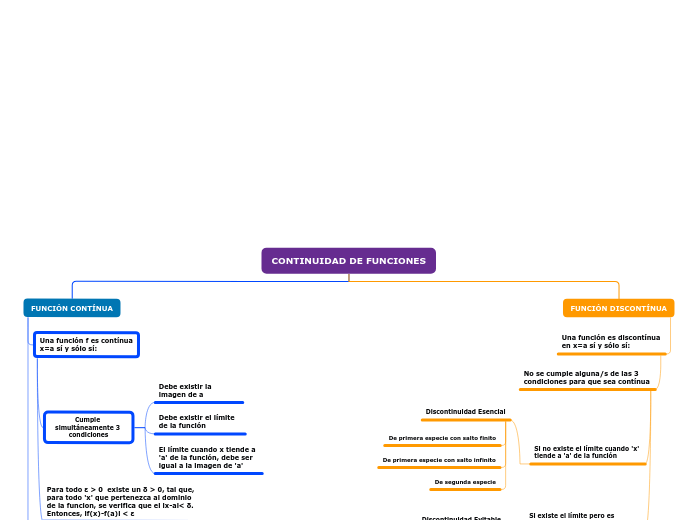
FUNCIÓN DISCONTÍNUA

Una función es discontínua en x=a sí y sólo sí:

No se cumple alguna/s de las 3 condiciones para que sea contínua

Si existe el límite pero es distinto de la imagen de 'a'

Discontinuidad Evitable

Si no existe el límite cuando 'x' tiende a 'a' de la función

Discontinuidad Esencial

De segunda especie

De primera especie con salto infinito

De primera especie con salto finito

FUNCIÓN CONTÍNUA

En un intervalo

Cerrado

[a;b]

Para todo 'c' que pertenece a (a;b) se verifica que el limite cuando 'x' tiende a 'c' de la función es igual a la imagen de 'c' y el límite cuando 'x' tiende a 'a' tanto por izquierda como por derecha de la funcion son iguales a la imagen de 'b'

f es contínua en [a;b] sí y sólo sí f es contínua en (a;b), es contínua a derecha en x=a y es contínua a izquierda en x=b

Abierto

(a;b)

Para todo 'c' que pertenece al intervalo, el limite cuando 'x' tiende a 'c' de la funcion, es igual a la imagen de 'c'

f es contínua en (a;b) sí y sólo sí f es contínua en todos los puntos interiores del intervalo

Límites laterales (por izquierda y por derecha)

f es contínua a IZQUIERDA en x=x0 si y sólo si el límite cuando 'x' tiende a x0 de la función es igual a la imagen de x0

f es contínua a DERECHA sí y sólo sí el límite cuando 'x' tiende a x0 de la función es igual a la imagen de x0

Una función f es contínua x=a sí y sólo sí:

Para todo ε > 0 existe un δ > 0, tal que, para todo 'x' que pertenezca al dominio de la funcion, se verifica que el lx-al< δ. Entonces, lf(x)-f(a)l < ε

Cumple simultáneamente 3 condiciones

El límite cuando x tiende a 'a' de la función, debe ser igual a la imagen de 'a'

Debe existir el límite de la función

Debe existir la imagen de a