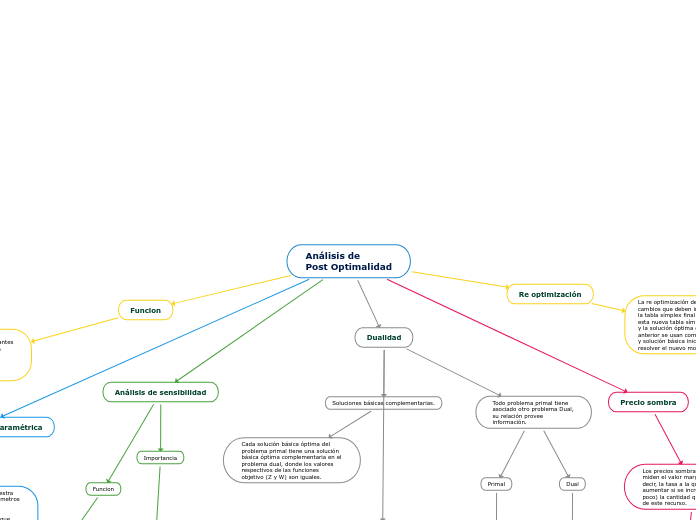
Análisis de
Post Optimalidad
Dualidad
Soluciones básicas complementarias.
Cada solución básica óptima del problema primal tiene una solución básica óptima complementaria en el
problema dual, donde los valores respectivos de las funciones objetivo (Z y W) son iguales.
Relaciones primal - dual
Dualidad fuerte
Si x* es una solución óptima para el problema primal y
y* es una solución óptima para el problema dual.
Soluciones complementarias
En cada iteración, el método símplex identifica de manera simultánea una solución FEV, x, para el problema primal y una solución complementaria, y, para el problema dual.
Dualidad debil
Si x es una solución factible para el problema primal y Y
es una solución factible para el problema dual.
Todo problema primal tiene asociado otro problema Dual, su relación provee información.
Primal
Problema original
Dual
Problema nuevo
Funcion
Busca evaluar parámetros (Constantes y coeficientes) para poder conocer los posibles puntos de mejora de nuestro sistema.
Re optimización
La re optimización deduce los cambios que deben introducirse a la tabla símplex final. A partir de esta nueva tabla símplex revisada y la solución óptima del modelo anterior se usan como tabla inicial y solución básica inicial para resolver el nuevo modelo.
Dentro de las ventajas de la re optimización es que quizá la solución óptima del problema revisado esté mucho más cerca de la solución óptima anterior que de una solución BF inicial construida como siempre por el método símplex.
Precio sombra
Los precios sombra del recurso miden el valor marginal de éste, es decir, la tasa a la que Z puede aumentar si se incrementa (un poco) la cantidad que se proporciona de este recurso.
Sería el equivalente a evaluar el cambio en la función objetivo por
trasladar las restricciones activas en las direcciones posibles hasta encontrarse con un
vértice distinto.
Solo las restricciones atantes tienen precios sombra.
Los cambios en B, debe ser ligeros, cambios mayores pudieran cambiar las restricciones.
Programación lineal paramétrica
Consiste en convertir nuestra solución optima en parámetros constantes y nuestros parámetros en variables restringidas, de manera que podemos ver cual sería el mejor escenario para nuestra solución óptima según los cambios que podemos hacer a nuestros parámetros.
Análisis de sensibilidad
Funcion
Con este se valúa las posibles variaciones en la pendiente de la función objetivo, para determinar que tanto puede cambiar la misma antes de causar un cambio en la base.
Importancia
Es esencial de casi todos los estudios de programación lineal, los valores de los parámetros que se emplean en el modelo original son sólo estimaciones de las condiciones futura, por lo que investigar el efecto que tendrían sobre la solución óptima en caso de que surjan otras condiciones.