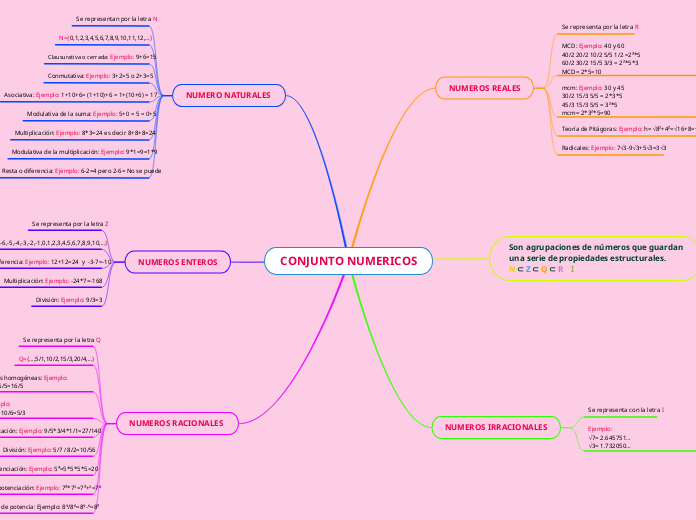
CONJUNTO NUMERICOS
NUMEROS REALES
Se representa por la letra R
MCD: Ejemplo: 40 y 60 40/2 20/2 10/2 5/5 1/2 =2³*5 60/2 30/2 15/5 3/3 = 2²*5*3 MCD= 2*5=10
mcm: Ejemplo: 30 y 45 30/2 15/3 5/5 = 2*3*5 45/3 15/3 5/5 = 3²*5 mcm= 2*3²*5=90
Teoría de Pitágoras: Ejemplo: h= √8²+4²=√16+8=√24=4.89897...
Radicales: Ejemplo: 7√3-9√3+5√3=3√3
Son agrupaciones de números que guardan una serie de propiedades estructurales. N ⊂ Z ⊂ Q ⊂ R I
NUMEROS IRRACIONALES
Se representa con la letra I
Ejemplo: √7= 2.645751... √3= 1.732050...
NUMERO NATURALES
Se representan por la letra N
N={0,1,2,3,4,5,6,7,8,9,10,11,12,...}
Clausurativa o cerrada: Ejemplo: 9+6=15
Conmutativa: Ejemplo: 3+2=5 o 2+3=5
Asociativa: Ejemplo: 1+10+6= (1+10)+6 = 1+(10+6) = 17
Modulativa de la suma: Ejemplo: 5+0 = 5 = 0+5
Multiplicación: Ejemplo: 8*3=24 es decir 8+8+8=24
Modulativa de la multiplicación: Ejemplo: 9*1=9=1*9
Resta o diferencia: Ejemplo: 6-2=4 pero 2-6= No se puede
NUMEROS ENTEROS
Se representa por la letra Z
Z={...,-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,10,...}
Suma o diferencia: Ejemplo: 12+12=24 y -3-7=-10
Multiplicación: Ejemplo: -24*7=-168
División: Ejemplo: 9/3=3
NUMEROS RACIONALES
Se representa por la letra Q
Q={...,5/1,10/2,15/3,20/4,...}
Suma o diferencia de fracciones homogéneas: Ejemplo: 8/5,3/5,5/5=8/5+3/5+5/5=8+3+5/5=16/5
Fracciones heterogéneas: Ejemplo: 8/4-2/6=48-8/24=40/24=20/12=10/6=5/3
Multiplicación: Ejemplo: 9/5*3/4*1/1=27/140
División: Ejemplo: 5/7 / 8/2=10/56
Potenciación: Ejemplo: 5⁴=5*5*5*5=20
Multiplicación de potenciación: Ejemplo: 7³*7⁵=7³+⁵=7⁸
División de potencia: Ejemplo: 8⁹/8⁶=8⁹-⁶=8³