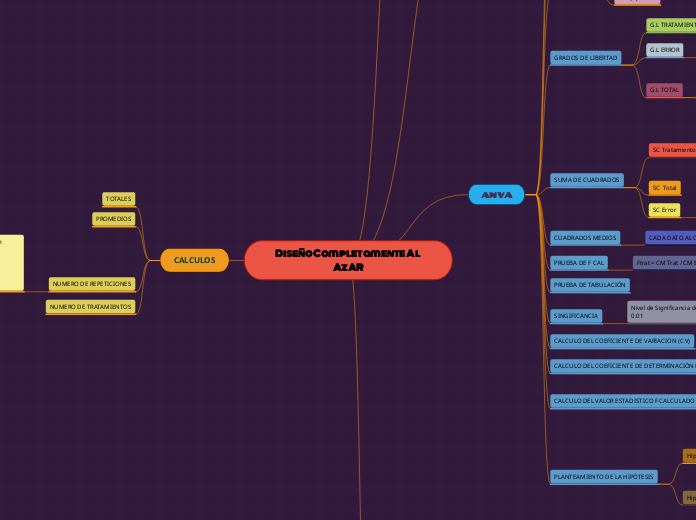
Diseño Completamente Al AzAR

Yij= U + TI + ERROR

ENUNCIADO DE PROBLEMA

VARIABLE DEPENDIENTE

VARIABLE INDEPENDIENTE

GRAN TOTAL

SUMA DE LOS TOTALES = G.T

FACTOR DE CORRECIÓN

BALANCEADO

FC = (G.T)^2 / r.t

NO BALANCEADO

GF.C = (G.T)^2 / n

NIVEL DE p

alfa (α) = 0.05

alfa (α) = 0.01

GRADOS DE LIBERTAD

G.L TRATAMIENTOS

t - 1

G.L ERROR

(r-1) * t

G.L TOTAL

DCA BALANCEADO

rt - 1

DCA NO BALANCEADO

n - 1

SUMA DE CUADRADOS

SC Tratamiento

DCA BALANCEADO

SC = (Totales)^2/r-FC

DCA NO BALANCEADO

SC = (Totales)^2/ni-FC

SC Total

SC Error

SC Error = SCTotal - SCTratamientos

CUADRADOS MEDIOS

CADA DATO AL CUADRADO

PRUEBA DE F CAL

Ftrat = CM Trat / CM Error

PRUEBA DE TABULACIÓN

SINGIFICANCIA

Nivel de Significancia del error: valor de p o Alfa α = 0.05, ó α = 0.01

CALCULO DEL COEFICIENTE DE VARIACION (C.V)

CV (%) = (RAIZ DE CM Error / Y) * 100 Y = Media general

CALCULO DEL COEFICIENTE DE DETERMINACIÓN R^2

R^2 = SCTratamientos/ SCTotal

CALCULO DEL VALOR ESTADISTICO F CALCULADO Fcal

Si Fcal < Ftab Acepto Ho

Si Fcal > Ftab Rechazo Ho

PLANTEAMIENTO DE LA HIPÓTESIS

Hipotesis Nula H0

Las dosis de fertilizantes tienen efecto
similar en el rendimiento de maíz en todos
losTratamientos, es decir:

Ho:A = B = C = D = E

Hipotesis Alterna. Hi

Al menos una de las dosis de fertilizantes tiene
efecto diferente en el rendimiento de del
maíz, es decir:

H1:A # B # C # D # E

tipos de pruebas de medias

prueba de la Diferencia Minima Significativa - DMS

prueba de DUNCAN

PRUEBA DE TUKEY

PRUEBA DE CONSTRASTE ORTOG

PRUEBA DE DUNNET

Pasos a Seguir

Cuadro de promedios y ANVA

1. ordenamiento de medias forma descendente

2. planteamiento de hipotesis

3. calculo del error estandar

4. calculo del valor critico de la prueba

PRUEBA DE COMPARACIÓN DE MEDIAS (DLS, DUNCAN, TUKEY)

5. comparación de la diferencia de promedios

6. cuadro de resultados y prueba de hipotesis

7. interpretación de resultados

8. conclusión

SDY = RAIZ DE 2CME / r

TOTALES

PROMEDIOS

NUMERO DE REPETICIONES

El número de repeticiones por tratamiento se escoge en función de:
-la variabilidad que se espera observar (exactitud en la medición)
, diferencia mínima detectable (la de interés por el experimentador)

NUMERO DE TRATAMIENTOS