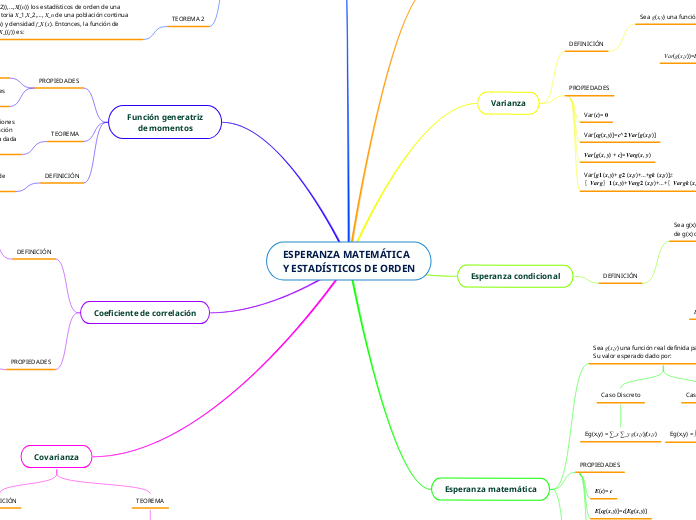
ESPERANZA MATEMÁTICA
Y ESTADÍSTICOS DE ORDEN

DEFINICIÓN

Sea X y Y variables aleatorias, la varianza condicional de Y dado X=x denotada por Var(y|x) es:

𝑉𝑎𝑟(𝑦│𝑥)=𝐸(𝑦^2│𝑥)−[𝐸(𝑦│𝑥)]^2

DEFINICIÓN

Sea 𝑔(𝑥,𝑦) una función real definida para toda 𝑥 y 𝑦.

𝑉𝑎𝑟(𝑔(𝑥,𝑦))=𝐸(𝑔(𝑥,𝑦))^2−[𝐸𝑔(𝑥,𝑦)]^2

PROPIEDADES

Var(𝒄)= 𝟎

Var[𝒄𝒈(𝒙,𝒚)]=𝒄^𝟐 𝑽𝒂𝒓[𝒈(𝒙,𝒚)]

𝑽𝒂𝒓[𝒈(𝒙, 𝒚) + 𝒄]=𝑽𝒂𝒓𝒈(𝒙, 𝒚)

Var[𝒈𝟏 (𝒙,𝒚)+ 𝒈𝟐 (𝒙,𝒚)+…+𝒈𝒌 (𝒙,𝒚)]≠
〖𝑽𝒂𝒓𝒈〗𝟏 (𝒙,𝒚)+𝑽𝒂𝒓𝒈𝟐 (𝒙,𝒚)+…+〖𝑽𝒂𝒓𝒈𝒌 (𝒙,𝒚)

DEFINICIÓN

Sea g(x) una función de X, entonces la esperanza condicional de g(x) dado Y=y denotada por 𝐸[𝑔(𝑥)│𝑦] esta dado por:

Caso Discreto

𝐸[𝑔(𝑥)|𝑦]= ∑_𝑥 𝑔(𝑥)𝑓(𝑥|𝑦)

Continuo

𝐸[𝑔(𝑥)|𝑦]=∫𝑥𝑔(𝑥)𝑓(𝑥|𝑦)𝑑𝑥

Sea 𝑔(𝑥,𝑦) una función real definida para toda 𝑥 y 𝑦.
Su valor esperado dado por:

Caso Discreto

Eg(x,y) = ∑_𝑥 ∑_𝑦 𝑔(𝑥,𝑦)𝑓(𝑥,𝑦)

Caso Continuo

Eg(x,y) = ∫∫〖𝑔(𝑥,𝑦)𝑓(𝑥,𝑦)𝑑𝑦𝑑𝑥,

PROPIEDADES

𝑬(𝒄)= 𝒄

𝑬[𝒄𝒈(𝒙,𝒚)]=𝒄[𝑬𝒈(𝒙,𝒚)]

𝑬[𝒈𝟏 (𝒙,𝒚)+ 𝒈𝟐 (𝒙,𝒚)+…+𝒈𝒌 (𝒙,𝒚)]
=〖𝑬𝒈〗𝟏 (𝒙,𝒚)+𝑬𝒈𝟐 (𝒙,𝒚)+…+〖𝑬𝒈〗𝒌 (𝒙,𝒚)

TEOREMA 2.2

Sean X y Y variables aleatorias independientes y
sean g(x) y h(y) funciones sólo de X y Y. Entonces:

𝑬[𝒈(𝒙)𝒉(𝒚)]=𝑬[𝒈(𝒙)] 𝑬[𝒉(𝒚)]

DEFINICIÓN

De una muestra aleatoria 𝑋1, 𝑋2, …, 𝑋𝑛 son los valores muestrales colocados en orden ascendente y se denotan por:
𝑋((1)),𝑋((2)),…,𝑋((𝑛))

Los estadísticos de orden son variables aleatorias que satisfacen que: 𝑋((1))≤𝑋((2) )≤…≤𝑋_((𝑛) )

TEOREMA 1

𝑃_𝑖 es una probabilidad acumulada, entonces:
Sea 𝑋((1)),𝑋((2)),…,𝑋((𝑛)) los estadísticos de orden de la muestra. Entonces:

𝑃(𝑋_((𝑗) )≤𝑥_𝑖 )=∑_(𝑘=𝑗)^𝑛〖((𝑛𝑘)) 𝑃𝑖^𝑘 (1−𝑃𝑖 )^(𝑛−𝑘) 〗

TEOREMA 2

Sea 𝑋((1)),𝑋((2)),…,𝑋((𝑛)) los estadísticos de orden de una muestra aleatoria 𝑋_1,𝑋_2,…, 𝑋_𝑛 de una población continua con fda 𝐹_𝑋 (𝑥) y densidad 𝑓_𝑋 (𝑥). Entonces, la función de densidad de 𝑋_((𝑗)) es:

𝑓(𝑋((𝑗) ) ) (𝑥)=𝑛!/(𝑗−1)!(𝑛−𝑗)! 𝑓𝑋 (𝑥) [𝐹𝑋 (𝑥)]^(𝑗−1) [1−𝐹𝑋 (𝑥)]^(𝑛−𝑗)

PROPIEDADES

2. La n-derivada de la función generatriz de momentos evaluada en 𝑡=0 es: 𝑀^𝑛 (0)=𝐸(𝑋^𝑛 )

1. La n-derivada de la función generatriz de momentos 𝑀(𝑡) es
𝑀_𝑋^𝑛 (𝑡)=𝑑/(𝑑𝑡^𝑛 ) 𝐸(𝑒^𝑡𝑋 )=𝐸(𝑑/(𝑑𝑡^𝑛 ) 𝑒^𝑡𝑋 )=𝐸(𝑋^𝑛 𝑒^𝑡𝑋 )

TEOREMA

Si X y Y son variables aleatorias independientes con funciones generatriz de momentos 𝑀_𝑋 (𝑡) y 𝑀_𝑌 (𝑡). Entonces la función generatriz de momentos la variable aleatoria 𝑍=𝑋+𝑌 esta dada por:

𝑀𝑍 (𝑡)=𝑀_𝑋 (𝑡) 𝑀𝑌 (𝑡)

DEFINICIÓN

Si X es una variable aleatoria con función de distribución acumulada 𝐹_𝑋. La función generatriz de momentos (fgm) de X, denotada por 𝑀_𝑋 (𝑡) , es:

𝑀𝑋 (𝑡)=𝐸𝑒^𝑡𝑋,

DEFINICIÓN

Si X y Y son variables aleatorias, el coeficiente de correlación de X y Y es el número definido por

𝜌𝑋𝑌=𝐶𝑜𝑟𝑟(𝑋, 𝑌)=𝐶𝑜𝑣(𝑋,𝑌)/√(𝑉𝑎𝑟(𝑋)𝑉𝑎𝑟(𝑌) )
=(𝐶𝑜𝑣(𝑋, 𝑌))/(𝜎𝑋 𝜎𝑌 )
donde |𝜌_𝑋𝑌 |≤1 o bien, 〖−1≤𝜌〗_𝑋𝑌≤1

PROPIEDADES

Si X y Y son independientes:
𝜌(𝑋, 𝑌) =0

-1 ≤ 𝜌(𝑋, 𝑌) ≤ 1

|𝜌(𝑋, 𝑌) | =1 cumpliendo restricciones.

DEFINICIÓN

Si X y Y son variables aleatorias con medias 𝜇𝑋 y 𝜇𝑌 respectivamente, la covarianza de X y Y es el número definido por
:

𝐶𝑜𝑣(𝑋,𝑌)=𝐸[(𝑋−𝜇𝑋 )(𝑌−𝜇𝑌 )]

TEOREMA

Para alguna variable aleatoria X y Y,:

𝐶𝑜𝑣(𝑋,𝑌)=𝐸𝑋𝑌−𝐸𝑋 𝐸𝑌