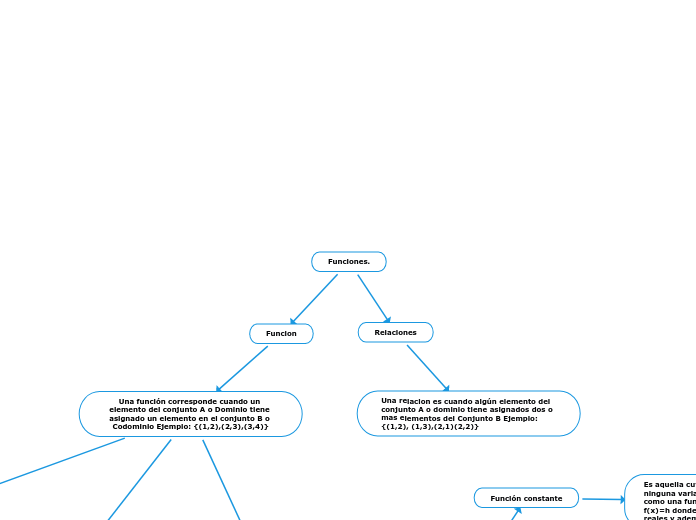
Funciones.
Funcion
Una función corresponde cuando un elemento del conjunto A o Dominio tiene asignado un elemento en el conjunto B o Codominio Ejemplo: {(1,2),(2,3),(3,4)}
Elementos de una Función
Una funcion de contar con dos conjuntos uno de ellos es llamado Dominio y otro elemento es llamado Codominio
Clasificación de las funciones
Funciones Inyectivas
Se dice que una funcion es inyectiva cuando a cada elemento del Dominio le corresponde un elemento del Codominio
Funciones suprayectivas
una función sobreyectiva, es cuando cada elemento del segundo conjunto (al que podemos llamar Codominio ) cuenta con, al menos, un elemento del primer conjunto Dominio.
Funciones Biyectivas
Una función es biyectiva si es al mismo tiempo inyectiva y sobreyectiva; es decir, si todos los elementos del conjunto del dominio tienen un valor distinto en el conjunto del codominio, y a cada elemento del conjunto del codominio le corresponde un elemento del conjunto del dominio
Tipo de funciones
Función constante
Es aquella cuyo valor no depende de ninguna variable, y se puede representar como una función matemática de la forma: f(x)=h donde h hace parte de los números reales y además es una constante.
Idéntica o Identidad
Es aquella cuya gráfica es una recta que pasa por el origen, de los ejes y sus coordenadas y su pendiente es m=1. se puede representar como F(x)=X
Valor Absoluto
Es aquella que se simboliza como |x| y transforma cualquier valor de x en su idéntico.
Por partes o trozos
Este tipo de funciones poseen un dominio definido por
varios intervalos y para cada uno de ellos, existe una regla que permite encontrar el correspondiente contra dominio. Se debe tomar cada parte como una función independiente
Función lineal
Una función lineal. se puede escribir esta expresión en la forma f(x) = mx+b, con m y b reales conocidos.
Cuadrática
forma f (x) =a2x2 + a1x + a0 con a2≠ 0, el dominio de esta función es el conjunto de los
números reales. Identificar los ceros de la función (si existen), significa dar solución a la
ecuación ax2+ bx + c =denominada como ecuación cuadrática.
Funcion Inversa
se tendría un elemento y, que poseería dos imágenes, lo cual contradice la definición de función
Funciones exponenciales
Una función de la forma f(x) = ax
con a un real positivo y diferente de 1, se denomina
una función exponencial de base.
Funciones logaritmicas
Es una función de la forma f(x) = aX se observa que es una función uno
a uno. Así que f tiene inversa
Relaciones
Una relacion es cuando algún elemento del conjunto A o dominio tiene asignados dos o mas elementos del Conjunto B Ejemplo: {(1,2), (1,3),(2,1)(2,2)}